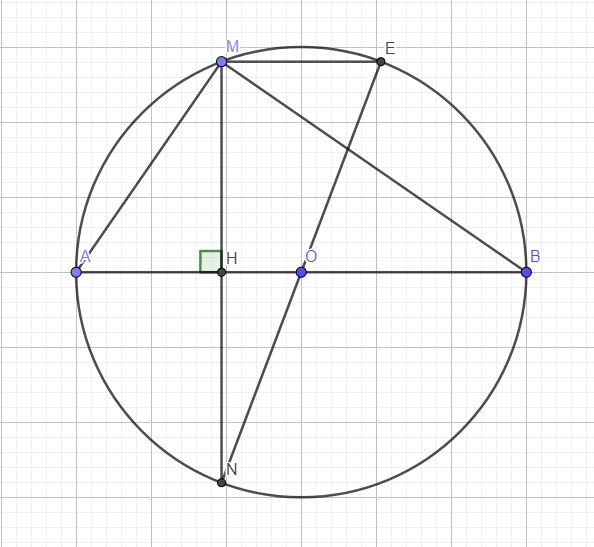
a.
Do \(ME||AB\Rightarrow\stackrel\frown{AM}=\stackrel\frown{EB}\) (hai dây song song chắn hai cung bằng nhau) (1)
Gọi H là giao điểm MN và AB
\(\Rightarrow H\) là trung điểm AB (đường kính vuông góc dây cung)
Trong tam giác AMN, AH vừa là đường cao vừa là trung tuyến
\(\Rightarrow\Delta AMN\) cân tại A \(\Rightarrow AM=AN\)
\(\Rightarrow\stackrel\frown{AM}=\stackrel\frown{AN}\) (2)
(1);(2) \(\Rightarrow\stackrel\frown{AM}=\stackrel\frown{AN}=\stackrel\frown{EB}\)
b.
Do \(\left\{{}\begin{matrix}ME||AB\\MN\perp AB\end{matrix}\right.\) \(\Rightarrow ME\perp MN\)
\(\Rightarrow\widehat{NME}=90^0\)
\(\Rightarrow\widehat{NME}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow NE\) là đường kính
\(\Rightarrow\) 3 điểm N, O, E thẳng hàng