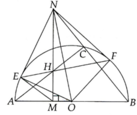
Cho nửa (O) đường kính AB. Lấy M Î OA (M không trùng O và A). Qua M vẽ đường thẳng d vuông góc với AB. Trên d lấy N sao cho ON > R. Nối NB cắt (O) tại C. Kẻ tiếp tuyến NE với (O) (E là tiếp điểm, E và A cùng thuộc nửa mặt phẳng bờ d). Chứng minh:
a, Bốn điểm O, E, M, N cùng thuộc một đường tròn
b, N E 2 = N C . N B
c, N E H ^ = N M E ^ (H là giao điểm của AC và d)
d, NF là tiếp tuyến (O) với F là giao điểm của HE và (O)
a, Học sinh tự chứng minh
b, N E C ^ = C B E ^ = 1 2 s đ C E ⏜
=> DNEC ~ DNBE (g.g) => ĐPCM
c, DNCH ~ DNMB (g.g)
=> NC.NB = NH.NM = N E 2
DNEH ~ DNME (c.g.c)
=> N E H ^ = E M N ^
d, E M N ^ = E O M ^ (Tứ giác NEMO nội tiếp)
=> N E H ^ = N O E ^ => EH ^ NO
=> DOEF cân tại O có ON là phân giác => E O N ^ = N O F ^
=> DNEO = DNFO vậy N F O ^ = N E O ^ = 90 0 => ĐPCM












