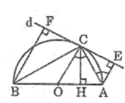
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên góc (ACB) = 90 °
Tam giác ABC vuông tại C có CH ⊥ AB
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
C H 2 = HA.HB (3)
Xét hai tam giác ACH và ACE, ta có:
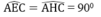
CH = CE (tính chất đường phân giác)
AC chung
Suy ra : ∆ ACH = ∆ ACE (cạnh huyền, cạnh góc vuông)
Suy ra: AH = AE (4)
Xét hai tam giác BCH và BCF, ta có:
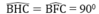
CH = CF (= CE)
BC chung
Suy ra: ∆ BCH = ∆ BCF (cạnh huyền, cạnh góc vuông)
Suy ra: BH = BF (5)
Từ (3), (4) và (5) suy ra: C H 2 = AE.BF









