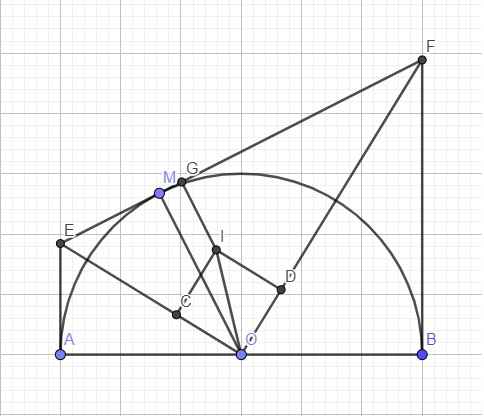
Cho nửa đường tròn (O,R) đường kính AB. Từ A và B kẻ hai tiếp tuyến Ax và By với nửa đường tròn. Gọi M là 1 điểm trên nửa đường tròn. Tiếp tuyến với nửa đường tròn tại M lần lượt cắt Ax, By tại E và F.
a) CMR AEMO là tứ giác nội tiếp
b) Gọi P,Q theo thứ tự là giao điểm của AM và OE, BM và OF. CMR MPOQ là hình chữ nhật
c) Gọi H là hình chiếu của M lên AB, K là giao điểm của MH và EB. So sánh MK và KH
d) Gọi r là bán kính đường tròn nội tiếp tam giác EOF. CMR 1/3 < r/R < 1/2
ai ko rảnh thì giúp mình cm r/R>1/3 ở ý d là dc r mik camon
Gọi I là tâm đường tròn nội tiếp EOF, C và D lần lượt là tiếp điểm của (I) với OE và OF
Tứ giác ICOD là hình chữ nhật (có 3 góc vuông)
Mà \(IC=ID=r\Rightarrow ICOD\) là hình vuông
\(S_{IEF}+S_{IEO}+S_{IFO}=\dfrac{1}{2}\left(IG.EF+IC.EO+ID.FO\right)\)
\(=\dfrac{1}{2}r\left(EF+EO+FO\right)\) (do \(IG=IC=ID=r\))
\(=S_{OEF}=\dfrac{1}{2}OM.EF=\dfrac{1}{2}R.EF\)
\(\Rightarrow\dfrac{r}{R}=\dfrac{EF}{EF+OE+OF}>\dfrac{EF}{EF+EF+EF}=\dfrac{1}{3}\)
(do tam giác OEF vuông nên \(OE< EF;OF< EF\))
tks bn nhiều nha