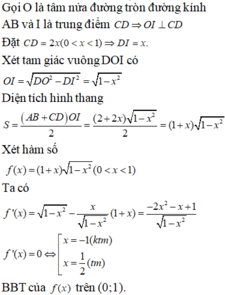Các câu hỏi tương tự
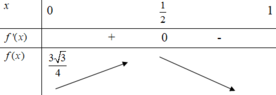
Cho nửa đường tròn đường kính AB và hai điểm C,D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng
Đọc tiếp
Cho nửa đường tròn đường kính AB và hai điểm C,D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng
![]()
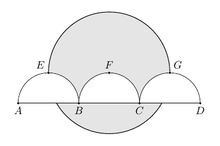
Trong hình vẽ dưới đây, đoạn AD được chia làm 3 bởi các điểm B và C sao cho AB BC CD 2. Ba nửa đường tròn có bán kính l là
AEB
⏜
,
BFC
⏜
và
CGD
⏜
có đường kính tương ứng là AB, BC và CD. Các điểm E, F, G lần lượt là tiếp điểm của tiếp tuyến chung EG với 3 nửa đường tròn. Một đường tròn tâm F, bán kính bằng 2. Diện tích miền bên trong đường tròn tâm F và bên ngoài...
Đọc tiếp
Trong hình vẽ dưới đây, đoạn AD được chia làm 3 bởi các điểm B và C sao cho AB= BC= CD= 2. Ba nửa đường tròn có bán kính l là AEB ⏜ , BFC ⏜ và CGD ⏜ có đường kính tương ứng là AB, BC và CD. Các điểm E, F, G lần lượt là tiếp điểm của tiếp tuyến chung EG với 3 nửa đường tròn. Một đường tròn tâm F, bán kính bằng 2. Diện tích miền bên trong đường tròn tâm F và bên ngoài 3 nửa đường tròn (miền tô đậm) có thể biểu diễn dưới dạng a b π - c + d , trong đó a, b, c, d là các số nguyên dương và a, b nguyên tố cùng nhau. Tính giá trị của a+b+c+d?
A. 14
B. 15
C. 16
D. 17
Cho nửa đường tròn đường kính AB 2R và điểm C thay đổi trên nửa đường tròn đó, đặt
α
C
A
B
⏞
và gọi H là hình chiếu vuông góc của C lên AB . Tìm
α
sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
Đọc tiếp
Cho nửa đường tròn đường kính AB = 2R và điểm C thay đổi trên nửa đường tròn đó, đặt α = C A B ⏞ và gọi H là hình chiếu vuông góc của C lên AB . Tìm α sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
![]()
![]()
![]()
![]()
Cho nửa đường tròn đường kính AB2R và điểm C thay đổi trên nửa đường tròn đó, đặt
α
C
A
B
^
và gọi H là hình chiếu vuông góc của C lên AB. Tìm
α
sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
Đọc tiếp
Cho nửa đường tròn đường kính AB=2R và điểm C thay đổi trên nửa đường tròn đó, đặt α = C A B ^ và gọi H là hình chiếu vuông góc của C lên AB. Tìm α sao cho thể tích vật thể tròn xoay tạo thành khi quay tam giác ACH quanh trục AB đạt giá trị lớn nhất.
![]()
![]()
![]()
![]()
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất. A.
A
D
2
2
a
B. ...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất.
A. A D = 2 2 a
B. A D = 4 a
C. A D = 4 3 3 a
D. A D = 2 a
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.
![]()
![]()
![]()
![]()
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
πcm
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
c
m
3
B.
60...
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 πcm . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho mặt cầu (S) có bán kính R 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu? A. 32
3
(
c
m
3
) B. 60
3...
Đọc tiếp
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Ta vẽ hai nửa đường tròn như hình bên, trong đó đường kính của nửa đường tròn lớn gấp đôi đường kính của nửa đường tròn nhỏ. Biết rằng nửa đường tròn đường kính AB có bán kính bằng 4 và
B
A
C
^
30
°
. Diện tích hình (H) (phần tô đậm) bằng:
Đọc tiếp
Ta vẽ hai nửa đường tròn như hình bên, trong đó đường kính của nửa đường tròn lớn gấp đôi đường kính của nửa đường tròn nhỏ. Biết rằng nửa đường tròn đường kính AB có bán kính bằng 4 và B A C ^ = 30 ° . Diện tích hình (H) (phần tô đậm) bằng:
![]()
![]()
![]()
![]()