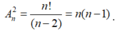
Chọn A
Hai điểm bất kì trong n điểm trên tạo thành hai véctơ thỏa mãn yêu cầu bài toán. Nên số các véc tơ đó là: 
Nhận xét: Có thể hiểu mỗi véctơ là một chỉnh hợp chập 2 của n điểm. Nên số véctơ là:
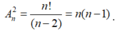
Cho hàm số y = x 3 + 3 x có đồ thị là (C) . M 1 là điểm trên (C) có hoành độ bằng 1. Tiếp tuyến tại điểm M 1 cắt (C) tại điểm M 2 khác M 1 . Tiếp tuyến tại điểm M 2 cắt (C) tại điểm M 3 khác M 2 . Tiếp tuyến tại điểm M n - 1 cắt (C) tại điểm M n khác M n - 1 ( n ≥ 4 , n ∈ ℕ )? Tìm số tự nhiên n thỏa mãn điều kiện y n - 3 x n + 2 21 = 0
A. n = 7
B. n = 8
C. n = 22
D. n = 21
Trên mặt phẳng cho 6 điểm phân biệt A, B, C, D, E; F. Hỏi có bao nhiêu vectơ khác vectơ – không, mà có điểm đầu và điểm cuối là các điểm đã cho ?
A. 100.
B. 120.
C. 30.
D. 25.
Trên mặt phẳng, cho bốn điểm phân biệt A, B, C, D. Liệt kê tất cả các vectơ khác vectơ – không mà điểm đầu và điểm cuối của chúng thuộc tập điểm đã cho.
Trong mặt phẳng cho 10 điểm phân biệt. Số vectơ khác 0 ⇀ , có điểm đầu và điểm cuối lấy trong các điểm đã cho là
A . 2 10
B . A 10 2
C. 10!
D . C 10 2
Cho hai đường thẳng d1 và d2 song song với nhau. Trên d1 có 10 điểm phân biệt, trên d2 có n điểm phân biệt n ≥ 2 . Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 20
B. 21
C. 30
D. 32
Cho hai đường thẳng d 1 và d 2 song song với nhau. Trên d 1 có 10 điểm phân biệt, trên d 2 có n điểm phân biệt ( n ≥ 2 ). Biết có 2800 tam giác có đỉnh là các điểm nói trên. Tìm n?
A. 16
B. 21
C. 30
D. 20
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n, biết rằng số tam giác có các đỉnh thuộc n + 6 điểm đã cho là 247.
Trên các cạnh AB, BC, CA của tam giác ABC lần lượt lấy 2, 4, n (n > 3) điểm phân biệt (các điểm không trùng với các đỉnh của tam giác). Tìm n biết rằng số tam giác có các đỉnh thuộc n+6 điểm đã cho là 247
A. 6
B. 7
C. 5
D. 8
Cho tâp ̣ A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Tìm n sao cho số tam giác mà 3 đỉnh thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A .
A. n = 6
B. n = 12
C. n = 8
D. n = 15
