Gọi x (cm) là độ dài đoạn AM.
Điều kiện: 0 < x < 12
Vì ΔABC vuông cân tại A nên ΔBMP vuông cân tại M.
Suy ra MP = MB = AB – AM = 12 – x (cm)
Diện tích hình bình hành MNCP bằng MP.MA = (12 – x)x ( c m 2 )
Theo đề bài, ta có phương trình:
(12 – x)x = 32 ⇔ x 2 – 12x + 32 = 0
∆ ' = - 6 2 – 1.32 = 36 – 32 = 4 > 0
∆ ' = 4 = 2
Cả hai giá trị của x đều thỏa mãn điều kiện bài toán
Vậy điểm M cách điểm A 8cm hoặc 4cm thì diện tích hình bình hành MNCP bằng 32 c m 2
Cho tam giác ABC có góc A=90 độ,trên BC lấy điểm M sao cho BM=MC.Trên AB lấy điểm N sao cho NP=NM.Trên tia đối của tia NM lấy P sao cho NP=NM.
a)chứng minh MN vuông góc với AB.
b)Tứ giác AMNP là hình gì?
c)chứng minh tứ giác APMC là hình bình hành.
d)Tam giác ABC có AB=AC thì tứ giác AMDP là hình gì?
e)Tam giac ABC có AB=AC,BC=12cm.Tính diện tích của tứ giác AMBP.
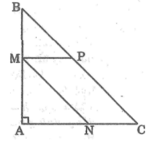
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
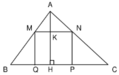
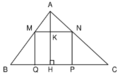
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
Các bạn giúp mình với
1> Cho hình thang ABCD có AB//CD , AC \(\ge\)BD và có diện tích hình thang bằng 1. Giá trị nhỏ nhất của AC co thể là bao nhiêu?
2. Cho tứ giác ABCD có AB+DC+AC = 10cm. Tính đường chéo BD biết diện tích tứ giác ABCD đạt max ?
3. Cho tam giác ABC vuông cân tại A. Hãy nội tiếp trong tm giác đó 1 hình chữ nhật có diện tích max
4. Cho hình vuông ABCd có độ dài 1 cạnh là a . Trên hai cạnh AD và aB lần lượt lấy 2 điểm M,N sao cho chu vi AMN là 2a Tìm vị trí điểm M và N đê diện tích tam giác AMN đạt max
5. Cho tam giác ABC có diện tích ko đổi Các đường phân giác trong cua các góc A,B,C lần lượt cắt các cạnh BC,AC,AB tại D,E,F. Xác định hình dạng tam giác ABC đê diện tích tam giác DÈF đạt max
6. Cho tam giác ABC, M ở trong tam giác các đường thẳng AM,BM,CM lần lượt cắt cách cạnh BC,AC,AB tại D,E,F. Xác định vị trí của điểm M để diện tích tam giác DEF đạt max
Cho tứ giác ABCD với D=90 độ, A=60 độ, B=150 độ, CD=12cm. AB là cạnh hình vuông có diện tích là 108cm^2. Miền trg tứ giác có điểm M sao cho ABCM là hình bình hành. MH vuông DC
a) CM:MC là phân giác BCD
b) DMC là tam giác vuông tại M
c) Tam giác AMD cân
d) Tính AD,BC=>Tam giác ADB đều
Các bạn giúp mình với
1> Cho hình thang ABCD có AB//CD , AC \(\ge\)BD và có diện tích hình thang bằng 1. Giá trị nhỏ nhất của AC co thể là bao nhiêu?
2. Cho tứ giác ABCD có AB+DC+AC = 10cm. Tính đường chéo BD biết diện tích tứ giác ABCD đạt max ?
3. Cho tam giác ABC vuông cân tại A. Hãy nội tiếp trong tm giác đó 1 hình chữ nhật có diện tích max
4. Cho hình vuông ABCd có độ dài 1 cạnh là a . Trên hai cạnh AD và aB lần lượt lấy 2 điểm M,N sao cho chu vi AMN là 2a Tìm vị trí điểm M và N đê diện tích tam giác AMN đạt max
5. Cho tam iacs ABC có diện tích ko đổi Các đường phân giác trong cua các góc A,B,C lần lượt cắt các cạnh BC,AC,AB tại D,E,F. Xác định hình dạng tam giác ABC đê diện tích tam giác DÈF đạt max
6. Cho tam giác ABC, M ở trong tam giác các đường thẳng AM,BM,CM lần lượt cắt cách cạnh BC,AC,AB tại D,E,F. Xác định vị trí của điểm M để diện tích tam giác DEF đạt max
Cho tam giác ABC cân tại A, hình vuông KLMN có đỉnh K trên cạnh AB, đỉnh L trên cạnh AC, các đỉnh M,N ở trên đáy BC
a) Tính tỉ số diện tích của tam giác và hình vuông khi tâm hình vuông trùng với trọng tâm tam giác
b) Tính cạnh hình vuông biết BC=16 ; AB=20
Giải bài toán hình lớp 9 Cho hình thang ABCD (AB//CD) nội tiếp (O) . Các đường chéo AC,BD cắt nhau tại E , các cạnh bên AD,BC kéo dài cắt nhau tại F. a) Chứng minh tam giác OAC= tam giác OBD b) Chứng minh tứ giác ADOE và tứ giác AOFC nội tiếp c) Gọi M,N theo thứ tự là trung điểm của BD,AC và P là hình chiếu của B lên dường thẳng CD.Chứng minh tứ giác MNCP là hình bình hành d) Cho góc DOC=120 độ , góc AOB=90 độ , tính diện tích tứ giác ABCD theo R
Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36 c m 2 .
Hình 17
Cho tam giác ABC có BC = 16cm , đường cao AH = 12 cm. Một hình chữ nhật MNPQ có đỉnh M thuộc cạnh AB, đỉnh N thuộc cạnh AC còn hai đỉnh P và Q thuộc cạnh BC (h.17). Xác định vị trí của điểm M trên cạnh AB sao cho diện tích của hình chữ nhật đó bằng 36cm2.
Hình 17
