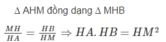Các câu hỏi tương tự
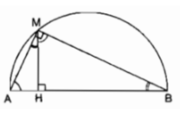
Cho một nửa đường tròn đường kính AB. Điểm M chạy trên nửa đường tròn. Kẻ MH vuông góc với AB tại H. Đặt MH = x. Chứng minh rằng hai tam giác AHM và MHB đồng dạng.
Cho một nửa đường tròn đường kính AB. Điểm M chạy trên nửa đường tròn. Kẻ MH vuông góc với AB tại H. Đặt MH = x. Khi M chuyển động thì x thay đổi, do đó tích AH.BH cũng thay đổi theo. Kí hiệu tích AH.BH bởi P(x). Hỏi P(x) có phải là một hàm số của biến số x hay không? Viết công thức biểu thị hàm số này..
Cho nửa đường tròn tâm O đường kính AB gọi Ax By là các tia vuông góc với AB Qua M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn đó cắt Ax By theo thứ tự tại C và D Chứng minh rằng
a, Kẻ MH vuông góc với AB tại H MH ra của ADN tại I Chứng minh I là trung điểm của MH
b, Tìm vị trí của M trên nửa đường tròn tâm O để chu vi ABCD đạt min
C, tìm vị trí của M trên nửa đường tròn tâm O để diện tích ABCD Đạt Min
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB gọi Ax By là các tia vuông góc với AB Qua M thuộc nửa đường tròn kẻ tiếp tuyến với nửa đường tròn đó cắt Ax By theo thứ tự tại C và D Chứng minh rằng
a, Kẻ MH vuông góc với AB tại H MH ra của ADN tại I Chứng minh I là trung điểm của MH
b, Tìm vị trí của M trên nửa đường tròn tâm O để chu vi ABCD đạt min
C, tìm vị trí của M trên nửa đường tròn tâm O để diện tích ABCD Đạt Min
Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đén AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C và D là các tiếp điểm khác H). Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi
Cho nửa đường tròn tâm (O) có đường kính AB 2R. Kẻ hai tiếp tuyến Ax , By của nửa đường tròn (O) tại A và B (Ax , By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn(M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D 1) Chứng minh tam giác COD vuông tại O 2) Chứng minh AC.BD R2 3)Kẻ MH vuông góc AB (H thuộc AB). Chứng minh rằng BC đi qua trung điểm của đoạn MHgiúp mik với
Đọc tiếp
Cho nửa đường tròn tâm (O) có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax , By của nửa đường tròn (O) tại A và B (Ax , By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn(M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D
1) Chứng minh tam giác COD vuông tại O
2) Chứng minh AC.BD = R2
3)Kẻ MH vuông góc AB (H thuộc AB). Chứng minh rằng BC đi qua trung điểm của đoạn MH
giúp mik với
Cho nửa đường tròn tâm O có đường kính AB 2R. Kẻ hai tiếp tuyến Ax. By của nửa đường tròn (O) tại A, B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn cắt tia Ax và By theo thứ tự tại C và D.A) chứng minh AC. BDR2B) kẻ MH vuông góc AB(H thuộc AB) chứng minh :OC song song với BM. C) chứng minh rằng BC đi qua trung điểm đoạn MH
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax. By của nửa đường tròn (O) tại A, B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn cắt tia Ax và By theo thứ tự tại C và D.
A) chứng minh AC. BD=R2
B) kẻ MH vuông góc AB(H thuộc AB) chứng minh :OC song song với BM.
C) chứng minh rằng BC đi qua trung điểm đoạn MH
Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đén AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C và D là các tiếp điểm khác H). Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi
3. Cho nửa đường tròn (o) đường kính AB , M là điểm tùy ý trên nửa đường tròn CM khác AB , kẻ MH vuông góc AB ( H thuộc AB ) , Trên cùng một nửa mặt phẳng bờ AB chứ nửa đường tròn . Vẽ 2 nửa đường tròn tâm O1 , đường kính AH và tâm O2 đường kính BH . MA và MB cắt 2 nửa đường tròn O1 và O2 lần lượt là P và Qa) chứng minh MHPQb) chứng minh tam giác MPQ và tam giác MBA đồng dạng c) chứng minh PQ là tiếp tuyến chung của 2 đường tròn O1 và O2 Giải giúp em với ạ ! em đang cần gấp bài này .
Đọc tiếp
3. Cho nửa đường tròn (o) đường kính AB , M là điểm tùy ý trên nửa đường tròn CM khác AB , kẻ MH vuông góc AB ( H thuộc AB ) , Trên cùng một nửa mặt phẳng bờ AB chứ nửa đường tròn . Vẽ 2 nửa đường tròn tâm O1 , đường kính AH và tâm O2 đường kính BH . MA và MB cắt 2 nửa đường tròn O1 và O2 lần lượt là P và Q
a) chứng minh MH=PQ
b) chứng minh tam giác MPQ và tam giác MBA đồng dạng
c) chứng minh PQ là tiếp tuyến chung của 2 đường tròn O1 và O2
Giải giúp em với ạ ! em đang cần gấp bài này .
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H
∈
AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm
O
1
, đường kính AH và tâm
O
2
, đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn (
O
1
) và...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H ∈ AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm O 1 , đường kính AH và tâm O 2 , đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn ( O 1 ) và ( O 2 ) lần lượt tại P và Q. Chứng minh:
a, MH = PQ
b, Các tam giác MPQ và MBA đồng dạng
c, PQ là tiếp tuyến chung của hai đường tròn ( O 1 ) và ( O 2 )