Question

Cho một hình chữ nhật ABCD. Trên AB lấy điểm M sao cho AM = MB, lấy điểm N trên BC sao cho BN gấp đôi NC. Hãy chứng tỏ rằng diện tích hình tam giác AMN bằng \(\frac{1}{6}\)diện tích hình chữ nhật ABCD.

Answer 1

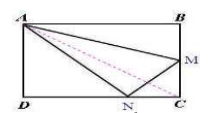
Ta có: \(S_{AMN}=\frac{BN.AM}{2}=\frac{BN\cdot\frac{1}{2}AB}{2}\)

\(S_{ABN}=\frac{AB.BN}{2}\)

=> \(\frac{S_{AMN}}{S_{ABN}}=\frac{\frac{\frac{1}{2}BN.AB}{2}}{\frac{AB.BN}{2}}=\frac{1}{2}\) => \(S_{AMN}=\frac{1}{2}S_{ABN}\)(1)

Ta lại có: BN = 2NC; BN + NC = BC => BN = 2/3BC

 \(S_{ABN}=\frac{AB.BN}{2}=\frac{AB\cdot\frac{2}{3}BC}{2}\)

\(S_{ABCD}=AB.BC\)

\(\frac{S_{ABN}}{S_{ABCD}}=\frac{\frac{\frac{2}{3}AB.BC}{2}}{AB.BC}=\frac{1}{3}\) => \(S_{ABN}=\frac{1}{3}S_{ABCD}\) => \(\frac{1}{2}S_{ABN}=\frac{1}{6}S_{ABCD}\)(2)

Từ (1) và (2) => \(S_{AMN}=\frac{1}{6}S_{ABCD}\)

Answer 2

awbb ưieaaaaaaaa

 r

ewfrsd

tf

sdfdyufee

e

ẻ

r

re

ê

r

e

ẻ

e

re

ẻ

rr