Các câu hỏi tương tự
Cho mặt cầu S(0;R) và mặt phẳng (
α
). Gọi d là khoảng cách từ O tới (
α
). Khi d R thì mặt phẳng (
α
) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng: A.
R
2
+
d
2
B.
R
2
-
d...
Đọc tiếp
Cho mặt cầu S(0;R) và mặt phẳng ( α ). Gọi d là khoảng cách từ O tới ( α ). Khi d < R thì mặt phẳng ( α ) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng:
A. R 2 + d 2 B. R 2 - d 2
C. R d d. R 2 - 2 d 2
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu? A.
R
d
B.
R
2
+
d
2
C.
R
2
-
d
2...
Đọc tiếp
Cho mặt cầu S(O;R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O;R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu? A.
R
d
B.
R
2
+
d
2
C.
R
2
-
d
2...
Đọc tiếp
Cho mặt cầu S(O; R) và mặt phẳng (α). Biết khoảng cách từ O tới (α) bằng d. Nếu d < R thì giao tuyến của mặt phẳng (α) với mặt cầu S(O; R) là đường tròn có bán kính bằng bao nhiêu?
A. R d
B. R 2 + d 2
C. R 2 - d 2
D. R 2 - 2 d 2
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1 0, (Q): 2x + y + z - 1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
3...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Tìm bán kính R của mặt cầu (S) tâm
I
-
1
;
2
;
4
biết (S) cắt mặt phẳng (Oxy) theo giao tuyến là đường tròn (C) có bán kính
r
2
.
Đọc tiếp
Tìm bán kính R của mặt cầu (S) tâm I - 1 ; 2 ; 4 biết (S) cắt mặt phẳng (Oxy) theo giao tuyến là đường tròn (C) có bán kính r = 2 .
![]()
![]()
![]()
![]()
Cho khối cầu (S) có tâm I và bán kính R
2
3
, gọi (P) là mặt phẳng cắt khối cầu (S) theo thiết diện là hình tròn (C) . Tính khoảng cách d từ I đến (P) sao cho khối nón có đỉnh I và đáy là hình tròn (C) có thể tích lớn nhất.
Đọc tiếp
Cho khối cầu (S) có tâm I và bán kính R= 2 3 , gọi (P) là mặt phẳng cắt khối cầu (S) theo thiết diện là hình tròn (C) . Tính khoảng cách d từ I đến (P) sao cho khối nón có đỉnh I và đáy là hình tròn (C) có thể tích lớn nhất.
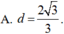
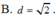
![]()
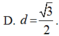
Cho mặt cầu (S) tâm O, bán kính R 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
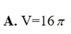
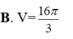
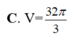
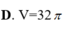
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng
(
α
)
cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai? A.
R
r
2
+
d
2
(
O
,
(
α
)
)...
Đọc tiếp
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng ( α ) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai?
A. R = r 2 + d 2 ( O , ( α ) )
B. d ( O , ( α ) ) < r
C. Diện tích của mặt cầu là S = 4 πr 2
D. Đường tròn lớn của mặt cầu có bán kính bằng bsn kính mặt cầu.
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .




