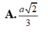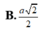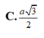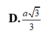Các câu hỏi tương tự
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R. Hỏi hình nón đó có bán kính r của đường tròn đáy và góc ở đỉnh của hình nón bằng bao nhiêu ?
Cho hình nón tròn xoay có đường cao h
5
bán kính đáy r 3. Mặt phẳng (P) qua đỉnh của hình nón nhưng không qua trục của hình nón và cắt hình nón theo giao tuyến là một tam giác cân có độ dài cạnh đáy bằng 4. Gọi O là tâm của hình tròn đáy. Tính khoảng cách d từ điểm O đến mặt phẳng (P).
Đọc tiếp
Cho hình nón tròn xoay có đường cao h = 5 bán kính đáy r = 3. Mặt phẳng (P) qua đỉnh của hình nón nhưng không qua trục của hình nón và cắt hình nón theo giao tuyến là một tam giác cân có độ dài cạnh đáy bằng 4. Gọi O là tâm của hình tròn đáy. Tính khoảng cách d từ điểm O đến mặt phẳng (P).
![]()
![]()
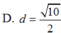
Cho
S
:
x
2
+
y
-
1
2
+
z
+
1
2
8
và
A
2
;
3
;
-
1...
Đọc tiếp
Cho S : x 2 + y - 1 2 + z + 1 2 = 8 và A 2 ; 3 ; - 1 . Xét mặt nón tròn xoay đỉnh A trục là IA( I là tâm mặt phẳng (S)) với góc ở đỉnh bằng 120 0 , đường tròn đáy hình nón thuộc mặt cầu. Viết phương trình mặt phẳng (P) chứa đường tròn đáy hình nón.
![]()
![]()
![]()
![]()
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R3cm, góc ở đỉnh của hình nón là
φ
120
0
. Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
Đọc tiếp
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh của hình nón là φ = 120 0 . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
![]()
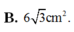
![]()
![]()
Cắt hình nón (N) đỉnh S cho trước bởi mặt phẳng qua trục của nó, ta được một tam giác vuông cân có cạnh huyền bằng
2
a
2
.
Biết BC là một dây cung đường tròn của đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng đáy của hình nón một góc
60
°
. Tính diện tích tam giác SBC.
Đọc tiếp
Cắt hình nón (N) đỉnh S cho trước bởi mặt phẳng qua trục của nó, ta được một tam giác vuông cân có cạnh huyền bằng 2 a 2 . Biết BC là một dây cung đường tròn của đáy hình nón sao cho mặt phẳng (SBC) tạo với mặt phẳng đáy của hình nón một góc 60 ° . Tính diện tích tam giác SBC.
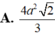
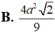
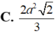
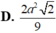
Cho khối nón tròn xoay có đường cao h 20 cm, bán kính đáy r 25 cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng: A. 500
c
m
2
B. 475
c
m
2
C. 450
c
m
2
D. 550...
Đọc tiếp
Cho khối nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm. Một mặt phẳng (P) chứa đỉnh S và giao tuyến với mặt phẳng đáy là AB. Khoảng cách từ tâm O của đáy đến mặt phẳng (P) là 12 cm. Khi đó diện tích thiết diện của (P) với khối nón bằng:
A. 500 c m 2
B. 475 c m 2
C. 450 c m 2
D. 550 c m 2
Một hình nón có góc ở đỉnh bằng 90°. Hình trụ có chung trục với hình nón. Một đáy của nó thuộc mặt đáy hình nón, đáy còn lại thuộc mặt xung quanh hình nón có bán kính bằng
2
3
bán kính đường tròn đáy hình nón. Tính
k
V
T
V
N
(VT, VN là thể tích hình trụ, hình nón).
Đọc tiếp
Một hình nón có góc ở đỉnh bằng 90°. Hình trụ có chung trục với hình nón. Một đáy của nó thuộc mặt đáy hình nón, đáy còn lại thuộc mặt xung quanh hình nón có bán kính bằng 2 3 bán kính đường tròn đáy hình nón. Tính k = V T V N (VT, VN là thể tích hình trụ, hình nón).
![]()
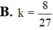
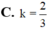
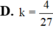
Cho hình nón
N
1
đỉnh S đáy là đường tròn C(O;R), đường cao SO40cm. Người ta cắt nón bằng mặt phẳng vuông góc với trục để được nón nhỏ
N
2
có đỉnh S và đáy là đường tròn C(O;R). Biết rằng tỷ số thể tích
V
N
2
V
N
1...
Đọc tiếp
Cho hình nón N 1 đỉnh S đáy là đường tròn C(O;R), đường cao SO=40cm. Người ta cắt nón bằng mặt phẳng vuông góc với trục để được nón nhỏ N 2 có đỉnh S và đáy là đường tròn C'(O';R'). Biết rằng tỷ số thể tích V N 2 V N 1 = 1 8 . Tính độ dài đường cao nón N 2 .
![]()
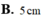
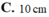
![]()
Cho hình nón đỉnh S có chiều cao h a và bán kính đáy r 2a. Mặt phẳng (P) đi qua S, không chứa trục của hình nón cắt đường tròn đáy tại A và B sao cho AB
2
3
a
.Khoảng cách từ âm của hình tròn đáy đến mặt phẳng (P) bằng
Đọc tiếp
Cho hình nón đỉnh S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S, không chứa trục của hình nón cắt đường tròn đáy tại A và B sao cho AB = 2 3 a .Khoảng cách từ âm của hình tròn đáy đến mặt phẳng (P) bằng

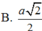
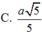
![]()