Chọn D.
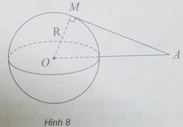
(h.8) Vì ∆ tiếp xúc với S(O;R) tại M nên OM ⊥ ∆ tại M.
Xét tam giác OMA vuông tại M, ta có:
AM 2 = OA 2 - OM 2 = d 2 - R 2
![]()
Chọn D.

(h.8) Vì ∆ tiếp xúc với S(O;R) tại M nên OM ⊥ ∆ tại M.
Xét tam giác OMA vuông tại M, ta có:
AM 2 = OA 2 - OM 2 = d 2 - R 2
![]()
Cho mặt cầu S(O; R) và điểm A cố định với OA = d. Qua A, kẻ đường thẳng tiếp xúc với mặt cầu S(O; R) tại M. Công thức nào sau đây được dùng để tính độ dài đoạn thẳng AM?
A. 2 R 2 - d 2
B. d 2 - R 2
C. R 2 - 2 d 2
D. d 2 + R 2
Cho mặt cầu S(O;R) và đường thẳng ∆ . Biết khoảng cách từ O tới ∆ bằng d. Với điều kiện nào sau đây thì đường thẳng ∆ tiếp xúc với mặt cầu S(O;R)?
A. d = R B. d > R
C. d < R D. d ≠ R
Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O;R) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
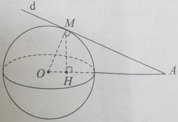
A. Mặt phẳng qua H và vuông góc với OA
B. Mặt phẳng trung trực của OA
C. Mặt phẳng qua O và vuông góc với AM
D. Mặt phẳng qua A và vuông góc với OM.
Từ điểm M nằm ngoài mặt cầu S(O;R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu?
A. 0 B. 1
C. 2 D. Vô số
I. Trắc nghiệm ( 6 điểm)
Cho mặt cầu S(O; R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
A. d = R
B. d > R
C. d < R
D. d ≠ R
Cho mặt cầu S(O;R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Đường thẳng Δ tiếp xúc với S(O; R) khi thỏa mãn điều kiện nào trong các điều kiện sau ?
A. d = R.
B. d > R
C. d < R.
D. d ≠ R.
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng AD 2 + BC 2 và AC 2 + BD 2 có giá trị không đổi
Cho mặt cầu (S) tâm O bán kính R và một đường thẳng d. Kí hiệu h là khoảng cách từ O đến đường thẳng d. Đường thẳng d có điểm chung với mặt cầu (S) nếu và chỉ nếu:
A. h ≤ R
B. h = R
C. h > R
D. h < R