Tuyển Cộng tác viên Hoc24 nhiệm kì 28 tại đây: https://forms.gle/GrfwFgzveoKLVv3p6
Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
( x - 1 ) 2 + ( y + 2 ) 2 + ( z + 3 ) 2 = 25
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -3); R = 25
B. I(-1; 2; 3); R = 5
C. I(-1; 2; 3); R = 25
D. I(1; -2; -3); R = 5
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x+4y-6z+90. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S). A. I(-1;2;3), R√5 B. I(1;-2;3), R√5 C. I(1;-2;3), R5 D. I(-1;2;-3), R5.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình x²+y²+z²-2x+4y-6z+9=0. Tìm tọa độ tâm I và tính bán kính R của mặt cầu (S).
A. I(-1;2;3), R=√5
B. I(1;-2;3), R=√5
C. I(1;-2;3), R=5
D. I(-1;2;-3), R=5.
Trong không gian với trục tọa độ Oxyz, cho
x
2
+
y
2
+
z
2
+2x-4y+6z-20 là phương trình mặt cầu (S). Mặt cầu
(
S
)
đồng tâm với mặt cầu (S) (có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M (1;3;-1). Khi đó, bán kính R của mặt cầu
(
S
)
bằng...
Đọc tiếp
Trong không gian với trục tọa độ Oxyz, cho x 2 + y 2 + z 2 +2x-4y+6z-2=0
là phương trình mặt cầu (S). Mặt cầu ( S ' ) đồng tâm với mặt cầu (S)
(có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M (1;3;-1). Khi đó,
bán kính R của mặt cầu ( S ' ) bằng bao nhiêu
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai đường thẳng
△
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và △ 2 : x - 2 = y + 3 = z 1 Trong tất cả các mặt cầu tiếp xúc với cả hai đường thẳng △ 1 và △ 2 Gọi (S) là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu (S) là
A. 12
B. 6
C. 24
D. 3
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x^2+y^2+z^2-6x bán kính R9 có phương trình là A.
(
x
+
4
)
2
+
(
y
-
5
)
2
+
(
z
+
6
)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x^2+y^2+z^2-6x bán kính R=9 có phương trình là
A. ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 9
B. ( x - 4 ) 2 + ( y + 5 ) 2 + ( z - 6 ) 2 = 81
C. ( x - 4 ) 2 + ( y + 5 ) 2 + ( z - 6 ) 2 = 9
D. ( x + 4 ) 2 + ( y - 5 ) 2 + ( z + 6 ) 2 = 81
Trong không gian Oxyz cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
2
)
2...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0 Gọi M là một điểm bất kì trên mặt cầu (S) Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
![]()
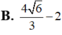
![]()
![]()
Trong không gian Oxyz, cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0. Gọi M là một điểm bất kì trên mặt cầu (S). Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
A. 4 6 3 - 2
B. 0
C. 6 - 2
D. 2 6 - 2
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1 0, (Q): 2x + y + z - 1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
3...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng
α
: x+y+z-40 và mặt cầu (S):
x
-
3
2
+
(
y
-
3
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng α : x+y+z-4=0 và mặt cầu (S): x - 3 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 16 Phương trình đường thẳng α đi qua M và nằm trong α cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng α đi qua điểm nào trong các điểm sau đây?
![]()
![]()
![]()
![]()



