Các câu hỏi tương tự
Cho I(2; -4; 1). Xác định bán kính R của mặt cầu (S) tâm I, cắt trục Oy tại A, B sao cho AB = 4
![]()
![]()
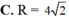
![]()
Mặt cầu (S) tâm I(1,2,4) cắt trục Oy tại 2 điểm A, B với
A
B
4
3
. Tính bán kính R của (S).
Đọc tiếp
Mặt cầu (S) tâm I(1,2,4) cắt trục Oy tại 2 điểm A, B với A B = 4 3 . Tính bán kính R của (S).
![]()
![]()
![]()
![]()
Cho hình cầu tâm O bán kính r. Lấy một điểm A trên mặt cầu và gọi ( α ) là mặt phẳng đi qua A sao cho góc giữa OA và ( α ) bằng 30 ° . Đường thẳng đi qua A vuông góc với mặt phẳng ( α ) cắt mặt cầu tại B. Tính độ dài đoạn AB.
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là: A.
(
x
-
1
)
2
+
(
y
-
...
Đọc tiếp
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là:
A. ( x - 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 9
B. ( x + 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 9
C. x 2 + y 2 + z 2 - 2x - 4y + 2z - 3 = 0
D. x 2 + y 2 + z 2 = 9
Trong không gian với trục tọa độ Oxyz, cho
x
2
+
y
2
+
z
2
+2x-4y+6z-20 là phương trình mặt cầu (S). Mặt cầu
(
S
)
đồng tâm với mặt cầu (S) (có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M (1;3;-1). Khi đó, bán kính R của mặt cầu
(
S
)
bằng...
Đọc tiếp
Trong không gian với trục tọa độ Oxyz, cho x 2 + y 2 + z 2 +2x-4y+6z-2=0
là phương trình mặt cầu (S). Mặt cầu ( S ' ) đồng tâm với mặt cầu (S)
(có tâm trùng với tâm mặt cầu (S)) và đi qua điểm M (1;3;-1). Khi đó,
bán kính R của mặt cầu ( S ' ) bằng bao nhiêu
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
Đọc tiếp
Trong không gian Oxyz, cho bốn điểm A(1;2;-4), B(1;-3;1), C(2;2;3), D(1;0;4). Gọi (S) là mặt cầu đi qua bốn điểmA,B,C,D. Tọa độ tâm I và bán kính R mặt cầu (S) là
![]()
![]()
![]()
![]()
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
Cho mặt cầu tâm O bán kính r. Gọi (
α
) là mặt phẳng cách tâm O một khoảng h (0 h r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng (
α
) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Đọc tiếp
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Cho
A
1
;
1
;
0
;
B
-
1
;
1
;
0
;
C
1
;
-
1
;
0
;
D...
Đọc tiếp
Cho A 1 ; 1 ; 0 ; B - 1 ; 1 ; 0 ; C 1 ; - 1 ; 0 ; D - 1 ; - 1 ; 0 là tâm của 4 mặt cầu có bán kính bằng 1. Gọi I là tâm mặt cầu (S) có bán kính bằng 1 tiếp xúc ngoài với cả 4 mặt cầu kể trên. Tính bán kính R của mặt cầu ngoại tiếp hình chóp I.ABCD.
![]()
![]()
![]()
![]()



