Các câu hỏi tương tự
Trong không gian Oxyz, cho mặt phẳng
α
:
2
x
+
3
y
-
2
z
+
12
0
. Gọi A, B, C lần lượt là giao điểm của
α
với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với
α
có phương trình là
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng α : 2 x + 3 y - 2 z + 12 = 0 . Gọi A, B, C lần lượt là giao điểm của α với 3 trục tọa độ, đường thẳng d đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với α có phương trình là
![]()
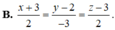
![]()
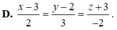
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(2;0;0) , B(1;-4;0), C(0;-2;6) và mặt phẳng ( α ) : x + 2y + z- 5 = 0. Gọi H(a;b;c) là hình chiếu vuông góc của trọng tâm tam giác ABC lên mặt phẳng ( α ) . Tính P = a - b + c.
A. 5
B. -3
C. 3
D. -1
Trong không gian Oxyz, cho mặt phẳng
(
α
)
: 2x + 3y - 2z + 12 0. Gọi A, B, C lần lượt là giao điểm của
(
α
)
với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với
(
α
)
có phương trình là A.
x
-
3
2
y
-
2
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2x + 3y - 2z + 12= 0. Gọi A, B, C lần lượt là giao điểm của ( α ) với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với ( α ) có phương trình là
A. x - 3 2 = y - 2 3 = z - 3 - 2
B. x + 3 2 = y - 2 - 3 = z - 3 2
C. x + 3 2 = y + 2 3 = z - 3 - 2
D. x - 3 2 = y - 2 3 = z + 3 - 2
Cho mặt cầu tâm O bán kính r. Gọi (
α
) là mặt phẳng cách tâm O một khoảng h (0 h r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng (
α
) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Đọc tiếp
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Một hình chữ nhật ABCD có AB a và
B
A
C
^
α
với
0
∘
α
90
∘
. Cho hình chữ nhật đó quay quanh cạnh AB, tam giác ABC tạo thành một hình nón có diện tích xung quanh là S. Mệnh đề nào là sai?
Đọc tiếp
Một hình chữ nhật ABCD có AB = a và B A C ^ = α với 0 ∘ < α < 90 ∘ . Cho hình chữ nhật đó quay quanh cạnh AB, tam giác ABC tạo thành một hình nón có diện tích xung quanh là S. Mệnh đề nào là sai?
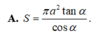
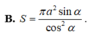
![]()
![]()
Cho hình lăng trụ đứng ABCABC có đáy ABC là tam giác cân,
A
B
A
C
α
,
B
A
C
^
120
°
,
B
B
α
, I là trung điểm của CC Gọi
α
là góc giữa hai mặt phẳng (ABC) và (ABI). Tính
cos
α
Đọc tiếp
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác cân, A B = A C = α , B A C ^ = 120 ° , B B ' = α , I
là trung điểm của CC' Gọi α là góc giữa hai mặt phẳng (ABC) và (AB'I). Tính cos α
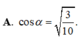
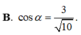

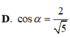
Cho mặt cầu tâm O bán kính r. Gọi (
α
) là mặt phẳng cách tâm O một khoảng h (0 h r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng (
α
) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).
Đọc tiếp
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Tìm tập hợp các điểm H, hình chiếu của B trên CD khi CD chuyển động trên đường tròn (C).
Trong không gian Oxyz, cho mặt phẳng
(
α
)
: x - z -3 0 và điểm M(1;1;1). Gọi A là điểm thuộc tia Oz, B là hình chiếu của A lên
(
α
)
. Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng A.
3
123
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : x - z -3 = 0 và điểm M(1;1;1). Gọi A là điểm thuộc tia Oz, B là hình chiếu của A lên ( α ) . Biết rằng tam giác MAB cân tại M. Diện tích của tam giác MAB bằng
A. 3 123 2
B. 6 3
C. 3 3 2
D. 3 3
Cho mặt cầu tâm O bán kính r. Gọi (
α
) là mặt phẳng cách tâm O một khoảng h (0 h r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng (
α
) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng
AD
2
+
BC
2
và...
Đọc tiếp
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Chứng minh các tổng AD 2 + BC 2 và AC 2 + BD 2 có giá trị không đổi