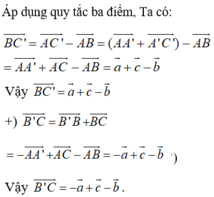Các câu hỏi tương tự
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc
60
0
. Tính thể tích khối lăng trụ ABC.A’B’C’
A
.
a
3
3
10
B
.
a
3...
Đọc tiếp
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A’B’C’
A . a 3 3 10
B . a 3 3 12
C . a 3 3 4
D . a 3 3 8
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc
45
0
. Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
A
.
a
3
3
10
B
.
a
3...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, đỉnh A’ cách đều ba đỉnh A, B, C. Cạnh bên AA’ tạo với đáy một góc 45 0 . Thể tích khối lăng trụ ABC.A’B’C’ bằng bao nhiêu?
A . a 3 3 10
B . a 3 3 12
C . a 3 4
D . a 3 8
Cho các vectơ
a
→
(4; -2),
b
→
(-1;-1),
c
→
(2;5). Phân tích vecto
b
→
theo hai vecto
a
→
và
c
→
ta được: A. B. C. D.
Đọc tiếp
Cho các vectơ a → = (4; -2), b → = (-1;-1), c → = (2;5). Phân tích vecto b → theo hai vecto a → và c → ta được:
A. 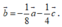
B. 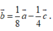
C. 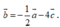
D. 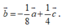
Cho khối lăng trụ đứng ABC.A’B’C’ có BB’ a, đáy ABC là tam giác vuông cân tại B, AB a. Tính thể tích V của khối lăng trụ.
Đọc tiếp
Cho khối lăng trụ đứng ABC.A’B’C’ có BB’ = a, đáy ABC là tam giác vuông cân tại B, AB = a. Tính thể tích V của khối lăng trụ.


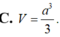
![]()
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
A
A
→
a
→
,
A
B
→
b
→
,
A
C
→
...
Đọc tiếp
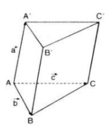
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt A A ' → = a → , A B → = b → , A C → = c →
Vecto B ' C → bằng:
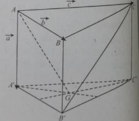
A. a → - b → - c →
B. c → - a → - b →
C. b → - a → - c →
D. a → + b → + c →
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
A
A
→
a
→
,
A
B
→
b
→
,
A
C
→
...
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt A A ' → = a → , A B → = b → , A C → = c →
Vecto A G → bằng:
A. a → + 1 / 6 ( b → + c → )
B. a → + 1 / 4 ( b → + c → )
C. a → + 1 / 2 ( b → + c → )
D. a → + 1 / 3 ( b → + c → )
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông tại C, BB’ a, góc
B
A
C
^
60
0
, đường thẳng BB tạo với (ABC) một góc
60
0
. Hình chiếu vuông góc của B lên (ABC) trùng với trọng tâm của tam giác ABC. Thể tích V của khối tứ diện A’ .ABC là:
Đọc tiếp
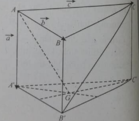
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông tại C, BB’= a, góc B A C ^ = 60 0 , đường thẳng BB' tạo với (ABC) một góc 60 0 . Hình chiếu vuông góc của B' lên (ABC) trùng với trọng tâm của tam giác ABC. Thể tích V của khối tứ diện A’ .ABC là:
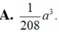
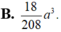
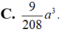
Cho lăng trụ ABC.A'B'C'.I,K lần lượt là trung điểm BB' và A'C.M được xác định bởi hệ thức vectơ MB= k*vectơ MC.Tìm k để 4 điểm A,I,M,K đồng phẳng
Cho lăng trụ đứng ABC.A’B’ C’ có đáy là tam giác vuông tại A,AC a và
A
C
B
^
60
0
; góc giữa BC’ và (AA’C) bằng
30
0
. Tính thể tích V của khối lăng trụ ABC.A’B’C’ A. V
a
3
6
B. V
2...
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’ C’ có đáy là tam giác vuông tại A,AC = a và A C B ^ = 60 0 ; góc giữa BC’ và (AA’C) bằng 30 0 . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = a 3 6
B. V = 2 a 3 6
C. V = a 3 3 6
D. V = a 3 6 2