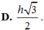Các câu hỏi tương tự
Cho lăng trụ đứng có chiều cao bằng h không đổi, một đáy là tứ giác ABCD với A ,B ,C ,D di động. Gọi I là giao của hai đường chéo AC và BD của tứ giác đó. Cho biết IA.IC IB.ID
h
2
. Tính giá trị nhỏ nhất bán kính mặt cầu ngoại tiếp hình lăng trụ đã cho.
Đọc tiếp
Cho lăng trụ đứng có chiều cao bằng h không đổi, một đáy là tứ giác ABCD với A ,B ,C ,D di động. Gọi I là giao của hai đường chéo AC và BD của tứ giác đó. Cho biết IA.IC = IB.ID = h 2 . Tính giá trị nhỏ nhất bán kính mặt cầu ngoại tiếp hình lăng trụ đã cho.
![]()
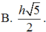
![]()
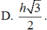
Cho lăng trụ ABC.ABC có đáy là tam giác vuông tại A, AB a và AC
a
2
. Biết rằng ((ABC),(ABC))
60
∘
và hình chiếu A lên (ABC) là trung điểm H của AB. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AHBC.
Đọc tiếp
Cho lăng trụ ABC.A'B'C' có đáy là tam giác vuông tại A, AB = a và AC = a 2 . Biết rằng ((ABC),(AB'C')) = 60 ∘ và hình chiếu A lên (A'B'C') là trung điểm H của A'B'. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AHB'C'.
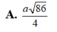
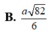
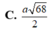
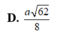
Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng: A. h
r
2
B. 2h
r
2
C. 3h
r
2
D. 4h
r
2
Đọc tiếp
Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng:
A. h r 2
B. 2h r 2
C. 3h r 2
D. 4h r 2
Cho hình lăng trụ tứ giác ABCD.ABCD có đáy ABCD là hình vuông cạnh a và thể tích bằng 3a3. Tính chiều cao h của hình lăng trụ đã cho. A. ha B. h9a C. h3a D. h a/3
Đọc tiếp
Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và thể tích bằng 3a3. Tính chiều cao h của hình lăng trụ đã cho.
A. h=a
B. h=9a
C. h=3a
D. h = a/3
Cho lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng 3a và chiều cao bằng 8a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AB’C’C.
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng 3a và chiều cao bằng 8a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AB’C’C.
![]()
![]()
![]()
![]()
Cho khối lăng trụ đứng tam giác ABC.ABC có đáy ABC là tam giác vuông tại A, ABa, ACa
3
, AA2a. Tính bán kính R của mặt cầu ngoại tiếp khối lăng trụ đó.
Đọc tiếp
Cho khối lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, AC=a 3 , AA'=2a. Tính bán kính R của mặt cầu ngoại tiếp khối lăng trụ đó.
![]()
![]()
![]()
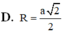
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Biết ABAA’a, AC2a. Gọi M là trung điểm của AC. Diện tích mặt cầu ngoại tiếp tứ diện MA’B’C’ bằng
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A. Biết AB=AA’=a, AC=2a. Gọi M là trung điểm của AC. Diện tích mặt cầu ngoại tiếp tứ diện MA’B’C’ bằng
![]()
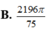
![]()
![]()
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại A, ABa
3
, BC2a. Đường thẳng AC tạo với mặt phẳng (BCCB) một góc 30
°
. Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a 3 , BC=2a. Đường thẳng AC' tạo với mặt phẳng (BCC'B') một góc 30 ° . Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
![]()
![]()
![]()
![]()
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại A, AB
a
3
, BC2a , đường thẳng AC tạo với mặt phẳng (BCCB) một góc 30
°
. Diện tích của mặt cầu ngoại tiếp lăng trụ đã cho bằng:
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C có đáy ABC là tam giác vuông tại A, AB= a 3 , BC=2a , đường thẳng AC' tạo với mặt phẳng (BCC'B') một góc 30 ° . Diện tích của mặt cầu ngoại tiếp lăng trụ đã cho bằng:
![]()
![]()
![]()
![]()