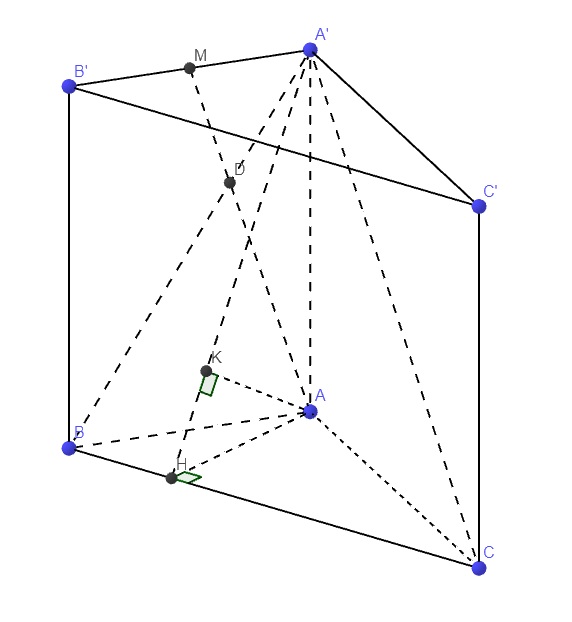
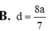Gọi D là giao điểm AM và A'B
Do \(A'B'||AB\), áp dụng định lý Thales:
\(\dfrac{MD}{DA}=\dfrac{MA'}{AB}=\dfrac{1}{2}\)
\(\left\{{}\begin{matrix}MA\cap\left(A'BC\right)=D\\\dfrac{MD}{DA}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(A'BC\right)\right)=\dfrac{1}{2}d\left(A;\left(A'BC\right)\right)\)
Từ A kẻ \(AH\perp BC\) (H thuộc BC)
Từ A kẻ \(AK\perp A'H\) (K thuộc \(A'H\))
\(\Rightarrow AK\perp\left(A'BC\right)\Rightarrow AK=d\left(A;\left(A'BC\right)\right)\)
Hệ thức lượng tam giác vuông ABC: \(AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Hệ thức lượng tam giác vuông A'AH:
\(AK=\dfrac{A'A.AH}{\sqrt{A'A^2+AH^2}}=\dfrac{2a\sqrt{57}}{19}\)
\(\Rightarrow d\left(M;\left(A'BC\right)\right)=\dfrac{1}{2}AK=\dfrac{a\sqrt{57}}{19}\)