Các câu hỏi tương tự
Cho lăng trụ
A
B
C
D
A
1
B
1
C
1
D
1
có đáy ABCD là hình chữ nhật với ABa, AD
a
3
Hình chiếu vuông góc của
A
1
lên ( ABCD) trung với giao điểm của AC và BD. Tính khoảng cách từ điểm B1 đến mặt phẳng (
A
1...
Đọc tiếp
Cho lăng trụ A B C D A 1 B 1 C 1 D 1 có đáy ABCD là hình chữ nhật với AB=a, AD= a 3 Hình chiếu vuông góc của A 1 lên ( ABCD) trung với giao điểm của AC và BD. Tính khoảng cách từ điểm B1 đến mặt phẳng ( A 1 B D )
A. a 3
B. a 2
C. a 3 2
D. a 3 6
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật: AB 2a, AD a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB;SC tạo với đáy góc
45
0
. Khoảng cách từ A đến mặt phẳng (SCD) là
A
.
a
3
3
B
.
a
6
4...
Đọc tiếp
Cho hình chóp S.ABCD đáy ABCD là hình chữ nhật: AB = 2a, AD = a. Hình chiếu của S lên mặt phẳng (ABCD) là trung điểm H của AB;SC tạo với đáy góc 45 0 . Khoảng cách từ A đến mặt phẳng (SCD) là
A . a 3 3
B . a 6 4
C . a 6 3
D . a 6 6
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD
120
0
và AA
7
a
2
. Hình chiếu vuông góc của A’ lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
Đọc tiếp
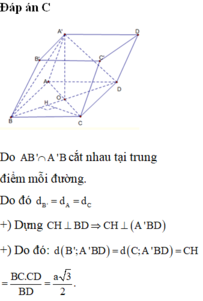
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD = 120 0 và AA' = 7 a 2 . Hình chiếu vuông góc của A’ lên mặt phẳng ABCD trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
![]()
![]()
![]()
![]()
Cho hình lăng trụ ABC.ABC có mặt đáy ABC là tam giác đều, độ dài cạnh AB 2a. Hình chiếu vuông góc của A lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng
60
0
, tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACCA)
A
.
h
39
a
13
B
.
...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 0 , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
A . h = 39 a 13
B . h = 2 15 a 5
C . h = 2 21 a 7
D . h = 15 a 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên đáy ABCD trùng với trọng tâm tam giác ABD. Mặt bên (SAB) tạo với đáy góc 60 ο . Tính theo a khoảng cách từ B đến mặt phẳng (SAD)
Cho khối lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông. Hình chiếu vuông góc của A trên mặt phẳng (ABCD) là trung điểm của AB, góc giữa mặt phẳng (A’CD) và mặt phẳng (ABCD) là
60
0
. Thể tích khối chóp B’.ABCD là
8
3
a
3
2...
Đọc tiếp
Cho khối lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông. Hình chiếu vuông góc của A trên mặt phẳng (ABCD) là trung điểm của AB, góc giữa mặt phẳng (A’CD) và mặt phẳng (ABCD) là 60 0 . Thể tích khối chóp B’.ABCD là 8 3 a 3 2 Tính độ dài đoạn thẳng AC theo a
A. 2 a 3 3
B. 2 3 a 3 3
C. 2a
D. 2 2 a
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB 2a; BC = \(\dfrac{3a}{2}\); AD = 3a. Hình chiếu vuông góc của S lên (ABCD) l;à trung điểm H của BD. Biết góc giữa (SCD) và (ABCD) bằng 60 độ. Tình khoảng cách từ C đến (SBD)?
Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc
B
A
D
60
o
. Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO 3a/4 . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).
Đọc tiếp
Hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có góc B A D = 60 o . Gọi O là giao điểm của AC và BD. Đường thẳng SO vuông góc với mặt phẳng (ABCD) và SO = 3a/4 . Gọi E là trung điểm của đoạn BC và F là trung điểm của đoạn BE.
a) Chứng minh mặt phẳng (SOF) vuông góc với mặt phẳng (SBC).
b) Tính các khoảng cách từ O và A đến mặt phẳng (SBC).