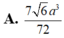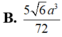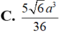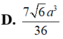Đáp án A
(ECD) chia A.BCD thành hai khối tứ diện A.ECD và E.BCD
Đáp án A
(ECD) chia A.BCD thành hai khối tứ diện A.ECD và E.BCD
Tiến hành phân chia khối lập phương ABCD.A'B'C'D', hỏi có bao nhiêu cách phân chia đúng trong các phương án sau:
i. Khối lăng trụ ABC.A'B'C', khối tứ diện AA'D'C' và khối chóp A.CDD'C'
ii. Khối tứ diện AA' B' D', khối tứ diện CC'D'B', khối chóp B'.ABCD
iii. Khối tứ diện A.A'B'C', khối chóp A.BCC'B' , khối lăng trụ ADC.A'D'C'
iv. Khối tứ diện AA'B'D', khối tứ diện C'CDB , khối chóp A.BDD'B', khối chóp C'.BDD'B'
A. 1
B. 2
C. 3
D. 4
Cho khối lăng trụ tam giác ABC. A 1 B 1 C 1 có đáy là tam giác đều cạnh a, A 1 A = a 2 và A 1 A tạo với mặt phẳng (ABC) một góc 30 o Tính thể tích khối tứ diện A 1 B 1 C A là
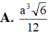
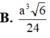
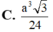
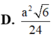
Cho khối chóp tứ giác S.ABCD. Gọi M là trung điểm của SC, mặt phẳng (P) chứa AM và song song BD chia khối lập phương thành hai khối đa diện, đặt V1 là thể tích khối đa diện có chứa đỉnh S và V2 là thể tích khối đa diện có chứa đáy ABCD. Tính V 2 V 1 .
A. V 2 V 1 = 3
B. V 2 V 1 = 1
C. V 2 V 1 = 2
D. V 2 V 1 = 3 2
Cho khối tứ diện ABCD. Lấy điểm M nằm giữa A và B, điểm N nằm giữa C và D. Bằng hai mặt phẳng (CDM) và (ABN), ta chia khối tứ diện đó thành bốn khối tứ diện nào sau đây ?
A. MANC, BCDN, AMND, ABND.
B. MANC, BCMN, AMND, MBND.
C. ABCN, ABND, AMND, MBND.
D. NACB, BCMN, ABND, MBND.
Cho hình lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông cân tại C với CA = CB = a. Trên đường chéo CA' lấy hai điểm M, N. Trên đường chéo AB' lấy được hai điểm P, Q sao cho MPNQ tạo thành một tứ diện đều. Tính thể tích khối lăng trụ ABC. A’B’C’
A. 2 a 3
B. a 3 6
C. a 3
D. a 3 2
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A, A B = a , A C = a 2 Biết rằng góc giữa hai mặt phẳng (AB’C’),(ABC) bằng 60 0 và hình chiếu A lên mặt phẳng (A'B'C') là trung điểm H của đoạn A’B’. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AHB’C’
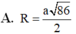
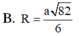

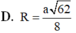
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh, a góc giữa mặt bên và mặt phẳng đáy là α thoả mãn cos α = 1 3 Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau
A. 0,11.
B. 0,13.
C. 0,7.
D. 0,9.
Cho khối tứ diện ABCD có ABC và BCD là các tam giác đều cạnh a. Góc giữa hai mặt phẳng (ABC) và (BCD) bằng 60 O . Tính thể tích V của khối tứ diện ABCD theo a:
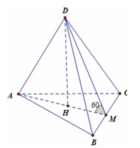
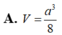
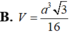
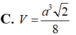
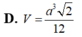
Cho khối chóp tứ giác đều S.ABCD có dạng đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Gọi M là điểm đối xứng với C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện ( H 1 ) và ( H 2 ), trong đó ( H 1 ) chứa điểm C. Thể tích của khối ( H 1 ) là: