Các câu hỏi tương tự
Cho khối trụ có bán kính đáy R và có chiều cao h 2R . Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O’. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O’) ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
Đọc tiếp
Cho khối trụ có bán kính đáy R và có chiều cao h = 2R . Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O’. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O’) ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
![]()
![]()
![]()
![]()
Cho hình trụ có hai đáy là hai đường tròn (O;R) và (O;R), chiều cao bằng đường kính đáy. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O lấy điểm B. Thể tích của khối tứ diện OOAB có giá trị lớn nhất bằng:
Đọc tiếp
Cho hình trụ có hai đáy là hai đường tròn (O;R) và (O';R), chiều cao bằng đường kính đáy. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm O' lấy điểm B. Thể tích của khối tứ diện OO'AB có giá trị lớn nhất bằng:
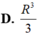
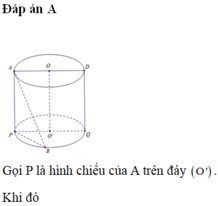
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt
α
là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
![]()
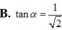
![]()
![]()
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt
α
là góc giữa AB và đáy. Tính
tan
α
khi thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. A.
tan
α
2
B.
tan
α...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt α là góc giữa AB và đáy. Tính tan α khi thể tích khối tứ diện OO’AB đạt giá trị lớn nhất.
A. tan α = 2
B. tan α = 1 2
C. tan α = 1 2
D. tan α = 1
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất. A.
A
D
2
2
a
B. ...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D trên đường tròn tâm O’ lấy điểm B, C sao cho AB//CD và AB không cắt OO’. Tính AD để thể tích khối chóp O’.ABCD đạt giá trị lớn nhất.
A. A D = 2 2 a
B. A D = 4 a
C. A D = 4 3 3 a
D. A D = 2 a
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho
A
D
2
3
a
; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt
α
là...
Đọc tiếp
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, D sao cho A D = 2 3 a ; gọi C là hình chiếu vuông góc của D lên mặt phẳng chứa đường tròn (O’); trên đường tròn tâm O’ lấy điểm B (AB chéo với CD) . Đặt α là góc giữa AB và đáy. Tính tan α khi thể tích khối tứ diện CDAB đạt giá trị lớn nhất.
A. tan α = 3
B. tan α = 1 2
C. tan α = 1
D. tan α = 3 3
Cho hình trụ có chiều cao ha
3
bán kính đáy ra. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng
30
0
. Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
Đọc tiếp
Cho hình trụ có chiều cao h=a 3 bán kính đáy r=a. Gọi O,O’ lần lượt là tâm của hai đường tròn đáy. Trên hai đường tròn đáy lần lượt lấy hai điểm A, B sao cho hai dường thẳng AB và OO’ chéo nhau và góc giữa hai đường thẳng AB với OO’ bằng 30 0 . Khoảng cách giữa hai đường thẳng AB và OO’ bằng :
![]()
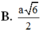
![]()
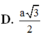
Cho hình trụ có tâm hai đáy lần lượt là O và O; bán kính đáy hình trụ bằng a. Trên hai đường tròn (O) và (O) lần lượt lấy hai điểm A và B sao cho AB tạo với trục của hình trụ một góc
30
°
và có khoảng cách tới trục của hình trụ bằng
a
3
2
. Tính diện tích toàn phần của hình trụ đã cho
Đọc tiếp
Cho hình trụ có tâm hai đáy lần lượt là O và O'; bán kính đáy hình trụ bằng a. Trên hai đường tròn (O) và (O') lần lượt lấy hai điểm A và B sao cho AB tạo với trục của hình trụ một góc 30 ° và có khoảng cách tới trục của hình trụ bằng a 3 2 . Tính diện tích toàn phần của hình trụ đã cho
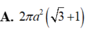
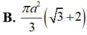
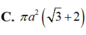
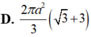
Một khối trụ có bán kính đáy bằng r và chiều cao bằng r
3
. Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 30
°
. Xác định và tính độ dài đoạn vuông góc chung của AB và trục của khối trụ.
Đọc tiếp
Một khối trụ có bán kính đáy bằng r và chiều cao bằng r 3 . Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 30 ° . Xác định và tính độ dài đoạn vuông góc chung của AB và trục của khối trụ.