Các câu hỏi tương tự
Trong không gian cho hình thang cân ABCD có AB//CD, AB a,CD 2a,AD a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
Đọc tiếp
Trong không gian cho hình thang cân ABCD có AB//CD, AB = a,CD = 2a,AD = a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
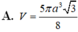
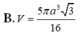
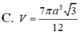
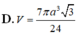
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
45
0
. Gọi
V
1
;
V
2
lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung đ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt bên (SAB) và (SAD) cùng vuông góc với mặt đáy. Biết góc giữa hai mặt phẳng (SCD) và (ABCD) bằng 45 0 . Gọi V 1 ; V 2 lần lượt là thể tích khối chóp S.AHK và S.ACD với H, K lần lượt là trung điểm cùa SC và SD. Tính độ dài đường cao của khối chóp S.ABCD và tỉ số k = V 1 V 2 .
A. h = a, k = 1 4
B. h =a , k = 1 6
C. h =2a, k = 1 8
D. h =2a, k = 1 3
Cho khối lăng trụ BAC.ABC. Mặt phẳng (P) đi qua C và các trung điểm của AA, BB chia khối lăng trụ thành hai khối đa diện có tỉ số thể tích bằng k với k
≤
1
. Tìm k. A.
1
3
B.
2
3
C.
1
D.
1
2
Đọc tiếp
Cho khối lăng trụ BAC.A'B'C'. Mặt phẳng (P) đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ thành hai khối đa diện có tỉ số thể tích bằng k với k ≤ 1 . Tìm k.
A. 1 3
B. 2 3
C. 1
D. 1 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho
S
M
S
B
S
N
S
D
k
. Tìm giá trị của k để thể tích khối chóp S.AMN bằng ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi và có thể tích bằng 2. Gọi M, N lần lượt là các điểm trên cạnh SB và SD sao cho S M S B = S N S D = k . Tìm giá trị của k để thể tích khối chóp S.AMN bằng 1 8
A. k = 1 8
B. k = 2 2
C. k = 2 4
D. k = 1 4
Cho hình hộp ABCD. A’B’C’D’ gọi O là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ A.
1
4
B.
1
3
C.
1
6
D.
1
12
Đọc tiếp
Cho hình hộp ABCD. A’B’C’D’ gọi O là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’
A. 1 4
B. 1 3
C. 1 6
D. 1 12
Cho tứ diện ABCD có
A
D
⊥
(
A
B
C
)
, đáy ABC thỏa mãn điều kiện Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC. Tính thể tích V của khối cầu ngoại tiếp khối chóp A. BCHK. A.
32
π
3
B.
8
π
3...
Đọc tiếp
Cho tứ diện ABCD có
A
D
⊥
(
A
B
C
)
, đáy ABC thỏa mãn điều kiện 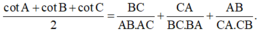
Gọi H, K lần lượt là hình chiếu vuông góc của A lên DB và DC.
Tính thể tích V của khối cầu ngoại tiếp khối chóp A. BCHK.
A. 32 π 3
B. 8 π 3
C. 4 π 3 3
D. 4 π 3
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Vecto M N → bằng:
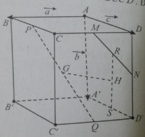
A. 1 2 c → - a →
B. 1 2 c → - b →
C. 1 2 b → - a →
D. 1 2 a → - b →
Cho hình hộp ABCD.A’B’C’D’ có A (1;0;0), B (2;-1;1), D (0;1;1) và A’ (1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thành bởi sáu điểm M, N, P, Q, E, F. A.
V
1
3
B.
V
1
2
C.
V
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có A (1;0;0), B (2;-1;1), D (0;1;1) và A’ (1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thành bởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a, AD 2a, AA’ 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP). A.
15
22
a
B.
9
11
a
C.
3
4
a
D.
15
11
a
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD =2a, AA’= 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP).
A. 15 22 a
B. 9 11 a
C. 3 4 a
D. 15 11 a