Các câu hỏi tương tự
Cho đa diện H biết rằng mỗi mặt của H đều là những đa giác có số cạnh lẻ và tồn tại ít nhất một mặt có số cạnh khác với các mặt còn lại. Hỏi khẳng định nào đúng trong các khẳng định sau? A. Tổng số các cạnh của (H) bằng 9 B. Tổng số các đỉnh của (H) bằng 5 C. Tổng số các cạnh của (H) là một số lẻ D. Tổng số các mặt của (H) là một số chẵn
Đọc tiếp
Cho đa diện H biết rằng mỗi mặt của H đều là những đa giác có số cạnh lẻ và tồn tại ít nhất một mặt có số cạnh khác với các mặt còn lại. Hỏi khẳng định nào đúng trong các khẳng định sau?
A. Tổng số các cạnh của (H) bằng 9
B. Tổng số các đỉnh của (H) bằng 5
C. Tổng số các cạnh của (H) là một số lẻ
D. Tổng số các mặt của (H) là một số chẵn
Có bao nhiêu loại khối đa điện đều mà mỗi mặt của nó là một tam giác đều?
A. 3.
B. 1.
C. 5.
D. 2.
Cho khối đa diện có tất cả các mặt đều là tam giác và các mệnh đề nào sau đây: (1). Số mặt của khối đa diện luôn là số chẵn. (2). Số cạnh của khối đa diện luôn là số lẻ. Khẳng định nào sau đây là đúng ? A. Chỉ có (1) đúng B. Cả (1) và (2) sai. C. Chỉ có (2) đúng. D. Cả (1) và (2) đúng.
Đọc tiếp
Cho khối đa diện có tất cả các mặt đều là tam giác và các mệnh đề nào sau đây:
(1). Số mặt của khối đa diện luôn là số chẵn. (2). Số cạnh của khối đa diện luôn là số lẻ.
Khẳng định nào sau đây là đúng ?
A. Chỉ có (1) đúng
B. Cả (1) và (2) sai.
C. Chỉ có (2) đúng.
D. Cả (1) và (2) đúng.
Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi C là số cạnh của khối đa diện đó, lúc đó ta có A. C là số chia hết cho 3 B. C là số chẵn C. C là số lẻ D. C là số chia hết cho 5
Đọc tiếp
Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi C là số cạnh của khối đa diện đó, lúc đó ta có
A. C là số chia hết cho 3
B. C là số chẵn
C. C là số lẻ
D. C là số chia hết cho 5
Cho đa giác đều 2019 đỉnh. Khi đó số tứ giác mà mỗi đỉnh được lấy từ các đỉnh của đa giác đều đã cho và không có cạnh nào là cạnh của đa giác đều đã cho là: A.
2019
C
2016
4
B.
2019
C
2019
4
- 2019 C. 504,75
2019
C
2016
4
D.
2019...
Đọc tiếp
Cho đa giác đều 2019 đỉnh. Khi đó số tứ giác mà mỗi đỉnh được lấy từ các đỉnh của đa giác đều đã cho và không có cạnh nào là cạnh của đa giác đều đã cho là:
A. 2019 C 2016 4
B. 2019 C 2019 4 - 2019
C. 504,75 2019 C 2016 4
D. 2019 C 2019 4
Cho khối đa diện đều n mặt có thể tích V và diện tích mỗi mặt của nó bằng S. Khi đó tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
Đọc tiếp
Cho khối đa diện đều n mặt có thể tích V và diện tích mỗi mặt của nó bằng S. Khi đó tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
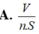
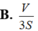
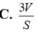
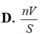
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
A
.
3
38
B
.
7
114
C
.
7
57
D
.
5
114
Đọc tiếp
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
A . 3 38
B . 7 114
C . 7 57
D . 5 114
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
Đọc tiếp
Cho đa giác đều 20 cạnh. Lấy ngẫu nhiên 3 đỉnh của đa giác đều. Xác suất để 3 đỉnh lấy được là 3 đỉnh của một tam giác vuông không có cạnh nào là cạnh của đa giác đều bằng
![]()
![]()
![]()
![]()
Cho hình đa diện đều loại {4;3} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
A
.
S
6
a
2
B
.
S
4
a
2
C
.
S
8
a
2...
Đọc tiếp
Cho hình đa diện đều loại {4;3} cạnh a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây đúng?
A . S = 6 a 2
B . S = 4 a 2
C . S = 8 a 2
D . S = 10 a 2
Cho đa giác lồi (H) có 10|cạnh. Có bao nhiêu tam giác mà mỗi đỉnh của nó là đỉnh của (H) và mỗi cạnh của tam giác đó không trùng với cạnh nào của (H)?




