Chọn C
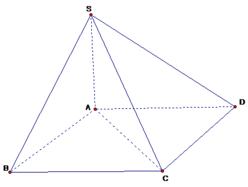
Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là : SABC,SACD
Chọn C

Mặt phẳng (SAC) chia khối chóp S.ABCD thành 2 khối tứ diện là : SABC,SACD
Cho khối chóp S.ABCD có đáy là hình bình hành. Mặt phẳng (SAC) chia khối chóp S.ABCD thành mấy khối tứ diện.
A. 2
B. 3
C. 4
D. 6
Cho khối chóp S.ABCD, hỏi hai mặt phẳng (SAC) và (SBD) chia khối chóp S.ABCD thành mấy khối chóp?
A. 4
B. 3
C. 5
D. 2
Cho khối chóp S.ABCD có đáy là hình bình bành thể tích bằng 1. Gọi M là điểm đối xứng của C qua B;N là trung điểm cạnh SC. Mặt phẳng (MDN) chia khối chóp S.ABCD thành hai khối đa diện, thể tích của khối đa diện chứa đỉnh S bằng
A. 5 6
B. 5 8
C. 12 19
D. 7 12
Khối chóp tứ giác S.ABCD có đáy là hình bình hành. Có bao nhiêu mặt phẳng cách đều cả 5 điểm S, A, B, C, D?
A. 5
B. 11
C. 9
D. 3
Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng 60 0 . Gọi M là điểm đối xứng vưới C qua D và N là trung điểm của cạnh SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai khối đa diện ( H 1 ) và ( H 2 ) trong đó ( H 1 ) chứa điểm C. Thể tích của khối ( H 1 ) là
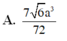
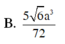
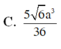
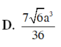
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi K,M lần lượt là trung điểm của các đoạn thẳng SA, SB, α là mặt phẳng qua K song song với AC và AM. Mặt phẳng α chia khối chóp S.ABCD thành hai khối đa diện. Gọi V1 là thể tích của khối đa diện chứa đỉnh S và V2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2 .
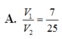
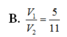
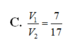
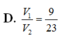
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tam giác SAC đều và nằm trong mặt phẳng vuông góc đáy. Tính thể tích khối chóp S.ABCD
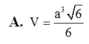
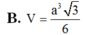
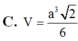
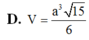
Cho khối chóp S.ABCD có đáy là hình bình hành, gọi B' và D' theo thứ tự là trung điểm các cạnh SB, SD. Mặt phẳng (AB'D') cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối đa diện được chia ra bởi mặt phẳng (AB'D')
A. 1 2
B. 1 6
C. 1 12
D. 1 5
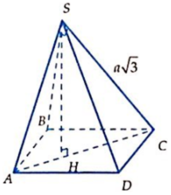
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD = 2a, mặt SAC là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC = a 3 . Tính thể tích khối chóp S.ABCD.
A. a 3 3 3
B. a 3 3 4
C. 2 a 3 3 3
D. a 3 3 6