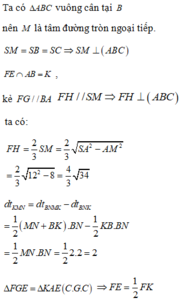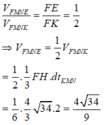Các câu hỏi tương tự
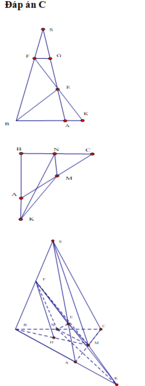
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết Tính thể tích V của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết 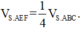 Tính thể tích V của khối chóp S.ABC
Tính thể tích V của khối chóp S.ABC
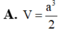
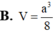
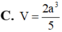
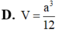
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A, B, C sao cho SA
1
2
SA; SB
1
3
SB; SC
1
4
SC. Gọi V và V lần lượt là thể tích của khối chóp S.ABC và S.ABC. Khi đó tỉ số
V
V
là: A. 12 B.
1
12
C. 24 D...
Đọc tiếp
Cho khối chóp S.ABC, trên ba cạnh SA, SB, SC lần lượt lấy ba điểm A', B', C' sao cho SA' = 1 2 SA; SB' = 1 3 SB; SC' = 1 4 SC. Gọi V và V' lần lượt là thể tích của khối chóp S.ABC và S.A'B'C'. Khi đó tỉ số V ' V là:
A. 12
B. 1 12
C. 24
D 1 24
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,ABa,SAperp AB,SCperp BC,SB2a.Gọi M,N lần lượt là trung điểm SA,BC. Gọi alpha là góc giữa MN với left(ABCright) .Tính cosalpha.
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(B,AB=a,SA\perp AB,SC\perp BC,SB=2a.\)Gọi \(M,N\) lần lượt là trung điểm \(SA,BC\). Gọi \(\alpha\) là góc giữa \(MN\) với \(\left(ABC\right)\) .Tính \(cos\alpha\).
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SASBSCa. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
Đọc tiếp
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có (SAB), (SAC) cùng vuông góc vưới mặt phẳng đáy, cạnh bên SB tạo với đáy một góc
60
0
. Đáy ABC là tam giác vuông cân tại B với Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện ABMNC
A
.
3
a
3
4
B
.
...
Đọc tiếp
Cho hình chóp S.ABC có (SAB), (SAC) cùng vuông góc vưới mặt phẳng đáy, cạnh bên SB tạo với đáy một góc 60 0 . Đáy ABC là tam giác vuông cân tại B với Gọi M, N lần lượt là trung điểm của SB, SC. Tính thể tích của khối đa diện ABMNC
A . 3 a 3 4
B . 3 a 3 6
C . 3 a 3 24
D . 3 a 3 8
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA 2a,
S
A
⊥
(
A
B
C
)
Gọi M, N lần lượt là trung điểm SA, SB và P là hình chiếu vuông góc của A lên SC. Tính thể tích V của khói chóp S.MNP. A.
a
3
3
30
B.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA= 2a, S A ⊥ ( A B C ) Gọi M, N lần lượt là trung điểm SA, SB và P là hình chiếu vuông góc của A lên SC. Tính thể tích V của khói chóp S.MNP.
A. a 3 3 30
B. a 3 3 6
C. a 3 3 15
D. a 3 3 10
Cho hình chóp S.ABC có SC 2a,
S
C
⊥
(
A
B
C
)
Đáy ABC là tam giác vuông cân tại B và có
(
α
)
Mặt phẳng
(
α
)
đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE. A.
4...
Đọc tiếp
Cho hình chóp S.ABC có SC= 2a, S C ⊥ ( A B C ) Đáy ABC là tam giác vuông cân tại B và có ( α ) Mặt phẳng ( α ) đi qua C và vuông góc với SA, cắt SA, SB lẩn lượt tại D, E. Tính thể tích khối chóp S.CDE.
A. 4 a 3 9
B. 2 a 3 3
C. 2 a 3 9
D. a 3 3
Cho hình chóp S.ABC. Trên các cạnh SA, SB, SC lần lượt lấy các điểm D, E, F (khác S). Gọi M là điểm chung của ba mặt phẳng (ABF), (BCD), (CAE). Đường thẳng SM lần lượt cắt các mặt phẳng (ABC) và (DEF) tại P và N. Chứng minh rằng \(\dfrac{NP}{NS}=3.\dfrac{MP}{MS}\)
Khối chóp chóp tam giác S.ABC có thể tích V. Gọi M,N,P lần lượt là trung điểm các cạnh SA, SB, SC. Thể tích của khối đa diện ABCMNP bằng A.
V
8
B.
3
V
4
C.
7
V
8...
Đọc tiếp
Khối chóp chóp tam giác S.ABC có thể tích V. Gọi M,N,P lần lượt là trung điểm các cạnh SA, SB, SC. Thể tích của khối đa diện ABCMNP bằng
A. V 8
B. 3 V 4
C. 7 V 8
D. V 4