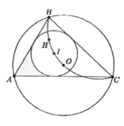
Chứng minh được B I C ^ = 120 0
=> B O C ^ = 2 B A C ^ = 120 0 => B H C ^ = 180 0 - 60 0 = 120 0 (góc nội tiếp và góc ở tâm)
=> H, I, O cùng nhìn BC dưới góc 120 0 nên B, C, O, I, H cùng thuộc một đường tròn
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60 ° . Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60 o . Gọi H là giao điểm của các đường cao BB'và CC'.
Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.
Cho tam giác ABC có góc A=600.Các điểm O,I lần lượt là tâm đường tròn ngoại tiếp,nội tiếp tam giác.Chứng minh rằng bốn điểm B,O,I,C cùng thuộc một đường tròn.
Cho tam giác ABC nội tiếp đường tròn (O;R).Quá tâm O vẽ các đường thẳng vuông góc với BC,AC lânf lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M,N;AM cắt BN tại I1.chứng minh 4 điểmO,H,C,K cùng thuộc một đường tròn2.chứng minh MN là trung trực của IC3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC.Tính bán kính đường tròn ngoại tiếp tam giác IBC theo R khi góc BAC120°
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O;R).Quá tâm O vẽ các đường thẳng vuông góc với BC,AC lânf lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M,N;AM cắt BN tại I
1.chứng minh 4 điểmO,H,C,K cùng thuộc một đường tròn
2.chứng minh MN là trung trực của IC
3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC.Tính bán kính đường tròn ngoại tiếp tam giác IBC theo R khi góc BAC=120°
Cho tam giác ABC nội tiếp đường tròn (O;R).Qua tâm O vẽ các đường thẳng vuông góc với BC,AC lần lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M,N1.chứng mình 4 điểm O,H,C,K cùng thuộc một đường tròn2.chứng minh MN là trung trực của IC3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC. Tính bán kính đường tròn ngoại tiếp tam giác IBC theo R khi góc BAC120°
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O;R).Qua tâm O vẽ các đường thẳng vuông góc với BC,AC lần lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M,N
1.chứng mình 4 điểm O,H,C,K cùng thuộc một đường tròn
2.chứng minh MN là trung trực của IC
3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC. Tính bán kính đường tròn ngoại tiếp tam giác IBC theo R khi góc BAC=120°
Cho tam giác ABC nội tiếp đường tròn (O;R).Quá tâm O vẽ các đường thẳng vuông góc vớiBC,AC lần lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M và N,AM cắt BN tại I1.chứng minh O,H,C,K cùng thuộc một đường tròn2.chứng minh MN là trung trực của IC3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC.Tính bán kính đường tròn ngoại tiếp IBC theo R khi góc BAC 120°
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O;R).Quá tâm O vẽ các đường thẳng vuông góc vớiBC,AC lần lượt tại H,K.Các đường thẳng này lần lượt cắt đường tròn tại M và N,AM cắt BN tại I
1.chứng minh O,H,C,K cùng thuộc một đường tròn
2.chứng minh MN là trung trực của IC
3.chứng minh M là tâm đường tròn ngoại tiếp tam giác IBC.Tính bán kính đường tròn ngoại tiếp IBC theo R khi góc BAC =120°
ho tam giác abc nội tiếp đường tròn (o,r) goi I là tâm của đường tròn nội tiếp tam giác đó gọi M N P lần lượt là tâm của các đường tròn bàng tiếp trong các góc A, B, C. gọi K là điểm đối xứng của I qua O. Chứng minh rằng K laftaam đường tròn ngoại tiếp tam giác MNP
Cho tam giác ABC có A bằng 60 độ .Các điểm O,I lần lượt là tâm đường tròn ngoại tiếp tam giác và nội tiếp tam giác.Chứng mình B,O,I,C cùng thuộc một đường tròn
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn tâm O. Gọi BD, CE là hai đường cao, H là trực tâm.
a) Chứng minh: ADHE, BEDC nội tiếp được.
b) Chứng minh: HB.HD=HE.HC
c) Các đường thẳng BD, CE cắt (O) lần lượt tại I và K. Chứng minh AC là đường trung trực của của HI.
d) Chứng minh: A là tâm đường tròn ngoại tiếp tam giác HIK.