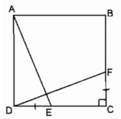
Xét ∆ ADE và ∆ DCF:
AD = DC (gt)
∠ A = ∠ D = 90 °
DE = CF (gt)
Do đó: ∆ ADE = ∆ DCF (c.g.c)
⇒ AE = DF
∠ (EAD) = ∠ (FDC)
∠ (EAD) + ∠ (DEA) = 90 ° (vì ΔADE vuông tại A)
⇒ ∠ (FDC) + ∠ (DEA) = 90 °
Gọi I là giao điểm của AE và DF.
Suy ra: ∠ (IDE) + ∠ (DEI) = 90 °
Trong ∆ DEI ta có: ∠ (DIE) = 180 ° – ( ∠ (IDE) + ∠ (DEI) ) = 180 ° – 90 ° = 90 °
Suy ra: AE ⊥ DF
cho hình bình hành ABCD. Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho AE=DF
a) Chứng minh AE//CF, BE//DF
b) chứng minh DE=DF
Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, trên cạnh DC lấy điểm E sao cho AF = DE. Chứng minh rằng AE = BF và AE ⊥ BF.
Cho hình vuông ABCD . Trên cạnh AB lấy điểm E , trên cạnh AD lấy điểm F sao cho AE=AF .Gọi I là giao điểm của DE và CF.
a. CMR : DE=CF và DE vuông góc với CF
b, Lấy P đối xứng với D qua I,lấy Q đối xứng với F qua I . Chứng minh tứ giác DEPQ là hình thoi.
Cho hình vuông ABCD. Trên các cạnh AB, AD lần lượt lấy 2 điểm E và F sao cho AE= DF. Đường thẳng
qua E và song song với AD cắt BD ở K. C/m:
a) AEKF là hình chữ nhật
b) DE = CF; DE vuông góc CF và EF = CK và EF vuông góc CK
c) Ba đường CK, BF và DE đồng qui.
Cho hình thoi ABCD. Lấy điểm E trên cạnh AB sao cho \(\dfrac{AE}{AB}=\dfrac{2}{3}\) và điểm F trên cạnh CD sao cho \(\dfrac{DF}{DC}=\dfrac{1}{3}\)
a) Tứ giác AECF, EBFD là hình gì?
b) AD và EF kéo dài gặp nhau ở H. Tính \(\dfrac{HD}{HA}\)
c) Chứng minh HC vuông góc với AC và F là trọng tâm tam giác HDB
Cho hình bình hành ABCD. Trên cạnh BC lấy điểm M sao cho và trên AB lấy điểm N sao cho AM=CN. Từ D kẻ DE vuông góc AM và DF vuông góc BN. Chứng minh: DE=DF.
Cho hình vuông ABCD ,trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm F sao cho AE=AF. Vẽ AH vuông góc với BF ( H thuộc BF ) , AH cắt DC và BC lần lượt tại hai điểm M,N
a, Chứng minh rằng tứ giác AEMD là hình chữ nhật
b, Biết diện tích tam giác BCH gấp 4 lần diện tích tam giác AEH. Chứng minh rằng :AC=2EF
c, Chứng minh rằng 1AD2=1AM2+1AN2
Cho hình bình hành ABCD. Trên cạnh AD lấy điểm E và trên cạnh CB lấy điểm E sao cho AE = CF. Chứng minh rằng hai điểm E, F đối xứng với nhau qua giao điểm của các đường chéo AC, BD.
Cho hình bình hành ABCD. Lấy điểm E trên cạnh AB, điểm F trên cạnh CD sao cho AE = CF. Chứng minh rằng ba đường thẳng AC, BD, EF đồng quy.
