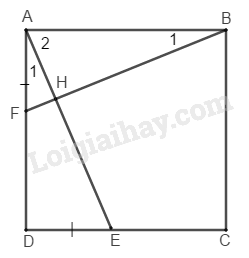
Xét ΔABF và ΔDAE ta có:
AB=DA (gt)
ˆBAF=ˆADE=900
AF=DE (gt)
Do đó: ΔABF=ΔDAE(c.g.c)
⇒BF=AE và ˆB1=ˆA1
Gọi H là giao điểm của AE và BF
ˆBAF=ˆA1+ˆA2=900
⇒ ˆB1+ˆA2=900
Trong ΔABH ta có:
ˆAHB+ˆB1+ˆA2=1800
ˆAHB=1800−(ˆB1+ˆA2)=1800−900=900
Vậy AE⊥BF
Xét ΔABF và ΔDAE ta có:
AB=DA (gt)
ˆBAF=ˆADE=900
AF=DE (gt)
Do đó: ΔABF=ΔDAE(c.g.c)
⇒BF=AE và ˆB1=ˆA1
Gọi H là giao điểm của AE và BF
ˆBAF=ˆA1+ˆA2=900
⇒ ˆB1+ˆA2=900
Trong ΔABH ta có:
ˆAHB+ˆB1+ˆA2=1800
ˆAHB=1800−(ˆB1+ˆA2)=1800−900=900
Vậy AE⊥BF






