Question

Cho hình vuông ABCD. Một góc \(EAF=45^0\) (E ∈ BC; F ∈ CD). Trên tia đối của tia DC lấy điểm G sao cho GD=BE.

a, Tính \(\widehat{FAG}\)  

b, C/m:  EF=BE+DF

Answer 1

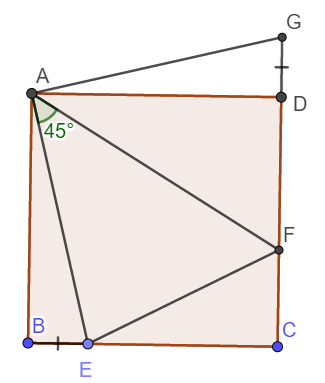
a) Xét tam giác vuông ABE và ADG có:

BE = DG (gt)

AB = AD

\(\Rightarrow\Delta ABE=\Delta ADG\)  (Hai cạnh góc vuông)

\(\Rightarrow\widehat{BAE}=\widehat{DAG}\)  (Hai góc tương ứng)

\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{DAG}+\widehat{FAD}\)

\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{FAG}\)

Mà \(\widehat{BAE}+\widehat{FAD}=90^o-\widehat{EAF}=45^o\) nên \(\widehat{FAG}=45^o\)

b) Do \(\Delta ABE=\Delta ADG\Rightarrow AE=AG\)

Xét tam giác AEF và AGF có:

AE = AG (cmt)

Cạnh AF chung

\(\widehat{EAF}=\widehat{GAF}\left(=45^o\right)\)

\(\Rightarrow\Delta AEF=\Delta AGF\left(c-g-c\right)\)

\(\Rightarrow EF=GF=FD+DG=FD+BE\)