a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
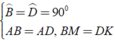
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
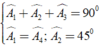
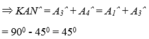

a) Áp dụng đĩnh nghĩa và giả thiết của hình vuông ABCD, ta được
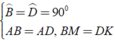
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
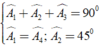
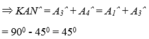
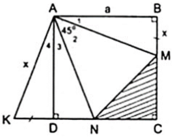
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Tính số đo K A N ^ = ?
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Tính số đo K A N ^ = ?
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính : Tính số đo K A N ^ = ?
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính : Chu vi tam giác MCN theo a.
Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho M A N ^ = 45 0 . Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính: Chu vi tam giác MCN theo a.
Cho hình vuông ABCD cạnh 6cm. Trên cạnh BC, CD lấy hai điểm M,N sao cho góc MAN= 45 độ. Trên tia đối của tia DC lấy điểm K sao cho DK=BM. Hãy tính a) số đo góc KAN
b) chu vi tam giác MCN
Cho hình vuông ABCD có cạnh là 6cm. Trên canh BC, CD lấy hai điểm M,N sao cho \(\widebat{MAN}=45^{\sigma}\). Trên tia đối của tia DC lấy điểm K sao cho DK =BM. Hãy tính: a) số đo góc KAN
b) CV \(\Delta MNC\)
o hình vuông ABCD cạnh bằng a. Lấy E trên BC, điểm F trên CD sao cho goác EAF= 45 độ. Trên tia đối DC lấy không sao cho DK = BE.
a. Tính số đo goác KAF
b. Tính chu vi góc CEF
=> làm cho mình câu b
Bài 1. Cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM = DN. a) Chứng minh tam giác AMN là tam giác vuông cân. b) Gọi E là trung điểm của MN. Tia AE cắt CD tại F. Chứng minh tam giác FAN = tam giác FAM.