Các câu hỏi tương tự
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay
-
90
0
biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC 3 thì IJ bằng bao nhiêu?
A
.
2
10
B
.
...
Đọc tiếp
Cho ba điểm A, B, C thẳng hang theo thứ tự đó và AB = 2BC. Dựng các hình vuông ABEF, BCGH (đỉnh của hình vuông tính theo chiều kim đồng hồ). Xét phép quay tâm B góc quay - 90 0 biến điểm E thành điểm A. Gọi I là giao điểm của EC và GH. Giả sử I biến thành điểm J qua phép quay trên. Nếu AC = 3 thì IJ bằng bao nhiêu?
A . 2 10
B . 5
C . 2 5
D . 10
Cho hình vuông ABCD tâm O(như hình vẽ).Phép quay tâm O, góc quay 630 ° ngược chiều kim đồng hồ. Biến:
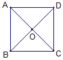
A. Điểm A thành điểm D
B. Điểm D thành điểm A
C. Điểm C thành điểm A.
D. Điểm C thành điểm D
Cho hình vuông ABCD (như hình vẽ). Phép quay tâm A góc quay
α
biến điểm D thành điểm B. Hỏi góc
α
à góc nào: A.
90
∘
B.-
90
∘
C.
45
∘
D. -
45
∘
Đọc tiếp
Cho hình vuông ABCD (như hình vẽ). Phép quay tâm A góc quay α biến điểm D thành điểm B. Hỏi góc α à góc nào:

A. 90 ∘
B.- 90 ∘
C. 45 ∘
D. - 45 ∘
Cho hình vuông ABCD, gọi O là giao điểm của AC và BD. Tìm ảnh của các điểm A, B, O qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc 90 ° và phép đối xứng qua đường BD (h.1.41).
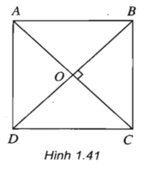
Cho hình vuông ABCD tâm O.
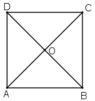
a. Tìm ảnh của điểm C qua phép quay tâm A góc 90 o .
b. Tìm ảnh của đường thẳng BC qua phép quay tâm O góc 90 o
Cho hình vuông ABCD tâm O. Phép quay nào sau đây biến hình vuông thành chính nó A.
Q
A
;
90
O
B.
Q
O
;
90
O
C.
Q
A
;...
Đọc tiếp
Cho hình vuông ABCD tâm O. Phép quay nào sau đây biến hình vuông thành chính nó
A. Q A ; 90 O
B. Q O ; 90 O
C. Q A ; 45 O
D. Q O ; 45 O
Cho hình vuông ABCD tâm O. Xác định ảnh của tam giác OBC qua phép quay tâm O góc quay 90°. a. Tam giácOCB b.tam giácOCD c.tam giácOAD d.tam giácOAB
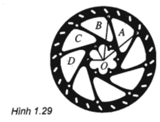
Trong hình 1.29 tìm một góc quay thích hợp để phép quay tâm O.
- Biến điểm A thành điểm B;
- Biến điểm C thành điểm D.
Với giá trị nào của góc
φ
sau đây thì phép quay
Q
O
;
φ
biến hình vuông ABCD tâm O thành chính nó? A.
φ
π
2
B.
φ
3
π
4
C.
φ
2
π...
Đọc tiếp
Với giá trị nào của góc φ sau đây thì phép quay Q O ; φ biến hình vuông ABCD tâm O thành chính nó?
A. φ = π 2
B. φ = 3 π 4
C. φ = 2 π 3
D. φ = π 3



