Các câu hỏi tương tự
Cho hai bộ ba điểm: A = (1; 3; 1), B = (0; 1; 2), C = (0; 0; 1). Hỏi bộ nào có ba điểm thẳng hàng?
B1 : a ) Người ta trồng 11 cây thành 10 hàng mỗi hàng có 3 cây b )Hãy trồng 10 cây thành 10 hàng mỗi hàng 3 cây B2 : Cho n điểm A1 , A2 , . . . An ( n 3 ) trong đó ko có điểm nào thẳng hàng , cứ qua 2 điểm ta vẽ đc một đường thẳng .a) Kể tên các đường thẳng trên hình nếu n5 b) Tính số đường thẳng trên hình nếu n20c)Tính số đường thẳng theo nd)Tính n nếu biết số đường thẳng kẻ đc là 2520B3 :a ) Cho n điểm phân biệt trong đó ko có 3 điểm nào thẳng hàng.Qua 2 điểm ta vẽ đc một đường thẳng . Có tấ...
Đọc tiếp
B1 :
a ) Người ta trồng 11 cây thành 10 hàng mỗi hàng có 3 cây
b )Hãy trồng 10 cây thành 10 hàng mỗi hàng 3 cây
B2 : Cho n điểm A1 , A2 , . . . An ( n > 3 ) trong đó ko có điểm nào thẳng hàng , cứ qua 2 điểm ta vẽ đc một đường thẳng .
a) Kể tên các đường thẳng trên hình nếu n=5
b) Tính số đường thẳng trên hình nếu n=20
c)Tính số đường thẳng theo n
d)Tính n nếu biết số đường thẳng kẻ đc là 2520
B3 :
a ) Cho n điểm phân biệt trong đó ko có 3 điểm nào thẳng hàng.Qua 2 điểm ta vẽ đc một đường thẳng . Có tất cả 28 đường thẳng . Tìm n ?
b)Cho n điểm phân biệt trong đó có 7 điểm thẳng hàng . Kẻ các đường thẳng đi qua các cặp điểm có tất cả 190 đường thẳng . Tìm n ?
c)Cho 20 đường thẳng đôi một cắt nhau và ko có ba đường thẳng nào đồng quy . Hỏi có bao nhiêu giao điểm tạo thành ?
Cho hai bộ ba điểm: M = (1; 1; 1), N = (-4; 3; 1), P = (-9; 5; 1). Hỏi bộ nào có ba điểm thẳng hàng?
Cho đường thẳng xy và điểm O không thuộc xy. Lấy n điểm A1;A2;......An. Vẽ các tia gốc O lần lượt đi qua A1;A2;.....An. Biết trên hình có tất cả 40 tia. Tính giá trị của n
Xem chi tiết
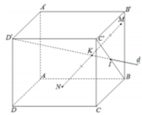
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCCB. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCCB) và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
Cho ba đoạn thẳng bẳng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều.
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng
α
song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là A. Một đường thẳng. B. Nửa đường thẳng. C. Đoạn thẳng song song với AB. D. Tập hợp rỗng.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm di động trên đoạn AB. Qua M vẽ mặt phẳng α song song với mặt phẳng (SBC), cắt các cạnh CD, DS, SA lần lượt tại các điểm N, P, Q. Tập hợp các giao điểm I của hai đường thẳng MQ và NP là
A. Một đường thẳng.
B. Nửa đường thẳng.
C. Đoạn thẳng song song với AB.
D. Tập hợp rỗng.
Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức
-
2
,
4
i
,
x
+
2
i
Với giá trị nào của x thì A, B, M thẳng hàng.
Đọc tiếp
Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức - 2 , 4 i , x + 2 i Với giá trị nào của x thì A, B, M thẳng hàng.
![]()
![]()
![]()
![]()
Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức -2, 4i, x+2i Với giá trị nào của x thì A, B, M thẳng hàng.
Đọc tiếp
Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức -2, 4i, x+2i Với giá trị nào của x thì A, B, M thẳng hàng.
![]()
![]()
![]()
![]()
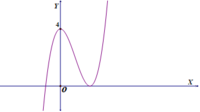
Cho hàm bậc ba y f(x) có đồ thị (C) như hình vẽ. Tổng tất cả các giá trị nguyên của m để đường thẳng y m cắt đồ thị (C) tại ba điểm phân biệt bằng: A. 6 B. 10 C. 9 D. 5
Đọc tiếp
Cho hàm bậc ba y =f(x) có đồ thị (C) như hình vẽ. Tổng tất cả các giá trị nguyên của m để đường thẳng y = m cắt đồ thị (C) tại ba điểm phân biệt bằng:
A. 6
B. 10
C. 9
D. 5





