Đáp án là A
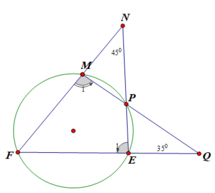
Xét tam giác NEF có: ∠F + ∠N + ∠ E 1 = 180 0 ⇒ ∠F + ∠E1 = 135 0
Xét tam giác FQM có: ∠F + ∠Q + ∠M1 = 180 0 ⇒ ∠F + ∠M1 = 145 0
Do FMPE là tứ giác nội tiếp nên ∠E1 + ∠M1 = 180 0
Do đó ta có: 2∠F + 180 0 = 280 0 ⇒ ∠F = 50 0
Đáp án là A

Xét tam giác NEF có: ∠F + ∠N + ∠ E 1 = 180 0 ⇒ ∠F + ∠E1 = 135 0
Xét tam giác FQM có: ∠F + ∠Q + ∠M1 = 180 0 ⇒ ∠F + ∠M1 = 145 0
Do FMPE là tứ giác nội tiếp nên ∠E1 + ∠M1 = 180 0
Do đó ta có: 2∠F + 180 0 = 280 0 ⇒ ∠F = 50 0

1.Trong hình 1, biết AC là đường kính, góc BDC bằng 600. Số đo góc ACB bằng
A. 400. | B. 450. | C. 350. | D. 300. |
2.Trong hình 2, góc QMN bằng 600, số đo góc NPQ bằng
A. 200. | B. 250. | C. 300. | D. 400. |
3.Trong hình 3, AB là đường kính của đường tròn, góc ABC bằng 600, khi đó số đo cung BmC bằng
A. 300. | B. 400. | C. 500. | D. 600. |
4.Trong hình 4, biết AC là đường kính của đường tròn, góc ACB bằng 300. Khi đó số đo góc CDB bằng
A. 400. | B. 500. | C. 600. | D. 700. |

5.Trên hình 5, biết số đo cung AmD bằng 800, số đo cung BnC bằng 300. Số đo của góc AED bằng
A. 250. | B. 500. | C. 550. | D. 400. |
6.Trong hình 6, số đo góc BIA bằng 600, số đo cung nhỏ AB bằng 550. Số đo cung nhỏ CD là
A. 750. | B. 650. | C. 600. | D. 550. |
7.Trên hình 7, có MA, MB là các tiếp tuyến tại A và B của (O). Số đo góc AMB bằng 580. Khi đó số đo góc OAB là
A. 280. | B. 290. | C. 300. | D. 310. |
8.Trên hình 8, số đo góc QMN bằng 200, số đo góc PNM bằng 100. Số đo của góc x bằng
A. 150. | B. 200. | C. 250. | D. 300 |

9.Trên hình 9, số đo cung nhỏ AD bằng 800. Số đo góc MDA bằng
A. 400. | B. 500. | C. 600. | D. 700. |
10.Trong hình 10, MA, MB là tiếp tuyến của (O), BC là đường kính, góc BCA bằng 700. Số đo góc AMB bằng
A. 700. | B. 600. | C. 500. | D. 400. |
11.Trong hình 11, có góc BAC bằng 200, góc ACE bằng 100, góc CED bằng 150. Số đo góc BFD bằng
A. 550. | B. 450. | C. 350. | D. 250. |
12.Trong hình 12, có AD//BC, góc BAD bằng 800, góc ABD bằng 600. Số đo góc BDC bằng
A. 400. | B. 600. | C. 450. | D. 650. |
Đố : Một hòn bi lăn trên một mặt phẳng nghiêng. Đoạn đường đi được liên hệ với thời gian bởi công thức y = a t 2 , t tính bằng giây, y tính bằng mét. Kết quả kiểm nghiệm được cho bởi bảng sau :
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 0,24 | 1 | 4 |
Biết rằng chỉ có một lần đo không cẩn thận, hãy xác định hệ số a và đố em biết lần nào đo không cẩn thận ?
* Tính ( không dùng máy tính)
\(\sin^235^0+tan22^0+sin^255^0-cotg13^0:tan77^0-cotg68^0\)
* Cho góc nhọn a, sina=\(\dfrac{2}{3}\)biết. Không tính số đo góc, hãy tính cosa, tân, cotga
Bài 2 (2,0 điểm ). Cho hàm số y = 2x - 4 a) Vẽ đồ thị (d) của hàm số y = 2x – 4. b) Tính khoảng cách từ 0 đến D . b) Xác định các hệ số a và b của hàm số y = ax + b (d') biết (d')//(d) và qua A (0;3)
1.Xác định các hệ số a,b,c Tính biệt thức \(\Delta\) từ đó áp dụng công thức nghiệm để giải các pt sau:
a. \(x^2-3x+2=0\)
b. \(-2x^2+x+1=0\)
c. \(x^2-4x+4=0\)
d. \(x^2-x+4=0\)
Trong hình vẽ, ta có đoạn thẳng A gấp khúc xếp thành hình lập phương, ở mỗi đỉnh lập phương nhỏ là một nguyên tử, tạo thành màng tinh thể đồng nhất. Na, K và các kim loại kiềm các chui vào mạng lưới. Có một nguyên tử A0 xác định tronmg một hình lập phương nhỏ, coi D0 là không gian tạo nên bởi các nguyên tử xung quanh gần sát A0 nhất, tính thể tich D0.
Trong hình vẽ, ta có đoạn thẳng A gấp khúc xếp thành hình lập phương, ở mỗi đỉnh lập phương nhỏ là một nguyên tử, tạo thành màng tinh thể đồng nhất. Na, K và các kim loại kiềm các chui vào mạng lưới. Có một nguyên tử A0 xác định trong một hình lập phương nhỏ, coi D0 là không gian tạo nên bởi các nguyên tử xung quanh gần sát A0 nhất, tính thể tích D0.
Trong hình vẽ, ta có đoạn thẳng A gấp khúc xếp thành hình lập phương, ở mỗi đỉnh lập phương nhỏ là một nguyên tử, tạo thành màng tinh thể đồng nhất. Na, K và các kim loại kiềm các chui vào mạng lưới. Có một nguyên tử A0 xác định trong một hình lập phương nhỏ, coi D0 là không gian tạo nên bởi các nguyên tử xung quanh gần sát A0 nhất, tính thể tích D0.
Trong hình vẽ, ta có đoạn thẳng A gấp khúc xếp thành hình lập phương, ở mỗi đỉnh lập phương nhỏ là một nguyên tử, tạo thành màng tinh thể đồng nhất. Na, K và các kim loại kiềm các chui vào mạng lưới. Có một nguyên tử A0 xác định tronmg một hình lập phương nhỏ, coi D0 là không gian tạo nên bởi các nguyên tử xung quanh gần sát A0 nhất, tính thể tich D0.