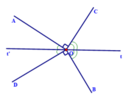
Ta có:
O C ⊥ O A ⇒ A O C ^ = 90 0
O B ⊥ O D ⇒ B O D ^ = 90 0
Ta có: Ot là tia phân giác của B O C ^
⇒ C O t ^ = t O B ^ = C O B ^ 2 ( t / c ) ⇒ C O B ^ = 2 C O t ^
Ta có: Ot' là tia phân giác của A O D ^
⇒ A O t ' ^ = t ' O D ^ = A O D ^ 2 ( t / c ) ⇒ A O D ^ = 2 A O t ' ^
Mặt khác: A O D ^ + D O B ^ + B O C ^ + A O C ^ = 360 0
⇒ 2 A O t ' ^ + 90 0 + 2 C O t ^ + 90 0 = 360 0
⇒ 2 A O t ' ^ + 2 C O t ^ = 180 0 ⇒ A O t ' ^ + C O t ^ = 90 0
Do đó: A O t ' ^ + A O C ^ + C O t ^ = 180 0
⇒ t ' O t ^ = 180 0
=> Ot và Ot' là hai tia đối nhau