Các câu hỏi tương tự
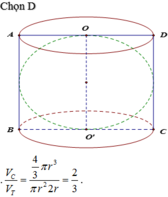
Hình trụ bán kính đáy r. Gọi O và O là tâm của hai đường tròn đáy với OO 2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ lại O và O. Gọi
V
C
và
V
T
lần lượt là thể tích của khối cầu và khối trụ. Khi đó là A.
1
2
B.
3
4
C.
2
3
D.
3...
Đọc tiếp
Hình trụ bán kính đáy r. Gọi O và O' là tâm của hai đường tròn đáy với OO' = 2r. Một mặt cầu tiếp xúc với hai đáy của hình trụ lại O và O'. Gọi V C và V T lần lượt là thể tích của khối cầu và khối trụ. Khi đó là
A. 1 2
B. 3 4
C. 2 3
D. 3 5
Khi cắt mặt cầu S(O;R) bởi một mặt kính, ta được hai nửa mặt cầu và hình tròn lớn của mặt kính đó gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R1,tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O;R) để khối trụ có thể tích lớn nhất.
Đọc tiếp
Khi cắt mặt cầu S(O;R) bởi một mặt kính, ta được hai nửa mặt cầu và hình tròn lớn của mặt kính đó gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R=1,tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O;R) để khối trụ có thể tích lớn nhất.
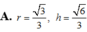
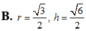
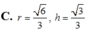
![]()
Khi cắt mặt cầu S(O;R) bởi một mặt kính, ta được hai nửa mặt cầu và hình tròn lớn của mặt kính đó gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R1,tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O;R) để khối trụ có thể tích lớn nhất.
Đọc tiếp
Khi cắt mặt cầu S(O;R) bởi một mặt kính, ta được hai nửa mặt cầu và hình tròn lớn của mặt kính đó gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S(O;R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R=1,tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S(O;R) để khối trụ có thể tích lớn nhất.
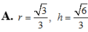
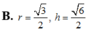
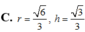
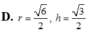
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
Đọc tiếp
Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.
![]()
![]()
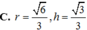
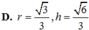
Cho hình trụ có hai đáy là hai hình tròn tâm O và O, bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn tâm O và O', bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O'. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
![]()
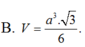
![]()
![]()
Cho hình trụ có hai đáy là hai hình tròn tâm O và O, bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn tâm O và O', bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O'. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.
![]()
![]()
![]()
![]()
Hình trụ tròn xoay có bán kính đáy bằng r, có chiều cao bằng 2r và có trục là OO’. Chứng minh rằng mặt cầu đường kính OO’ tiếp xúc với hai mặt đáy của hình trụ và tiếp xúc với tất cả các đường sinh của mặt trụ.
Cho khối trụ có chiều cao h16 và hai đáy là hình tròn tâm O, O với bán kính R12. Gọi I là trung điểm của OO và AB là một dây cung của đường tròn (O) sao cho
A
B
12
3
. Tính diện tích thiết diện của khối trụ với mặt phẳng (IAB).
Đọc tiếp
Cho khối trụ có chiều cao h=16 và hai đáy là hình tròn tâm O, O' với bán kính R=12. Gọi I là trung điểm của OO' và AB là một dây cung của đường tròn (O) sao cho A B = 12 3 . Tính diện tích thiết diện của khối trụ với mặt phẳng (IAB).
![]()
![]()
![]()
![]()
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h r
2
. Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Chứng minh rằng (
α
) tiếp xúc với mặt trụ trục OO’ có bán kính bằng
r
2
2
dọc theo một đường si...
Đọc tiếp
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao h = r 2 . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B. Chứng minh rằng ( α ) tiếp xúc với mặt trụ trục OO’ có bán kính bằng r 2 2 dọc theo một đường sinh.