Ta có (A; AD) và (C; CB) có bán kính AD = CB là cạnh của hình thoi ABCD nên hai đường tròn đó bằng nhau.
Vì CD = CB, suy ra D thuộc (C; CB)
Vì AB = AD, suy ra B thuộc (A; AD)
Suy ra (A; AD) và (C; CB) cắt nhau tại B và D.
DE // BF (gt)
cho hình vuông ABCD. Đường tròn đường kính CD và cung tròn tâm A bán kính AD cắt nhau tại M (M khác D)
a)CMR đường thẳng DM đi qua trung điểm I của BC
b)Gọi O là tâm đường tròn đường kính CD, gọi K là giao điểm của AO và DI. CMR DK.AI=2OD^2
c)Vẽ cung tròn BD có tâm C, trên cung BD lấy điểm F bất kỳ tia CF cắt đường tròn đường kính CD ở E. CM EF bằng khoảng cách từ F đến AD
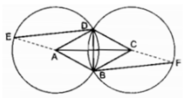
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E. So sánh hai cung BE và CD.
Cho tam giác đều ACB và ACD, cạnh a. Lần lượt lấy B và D làm tâm vẽ hai đường tròn bán kính a. Kẻ các đường kính ABE và ADF. Trên cung nhỏ CE của đường tròn tâm B lấy điểm M (không trùng với E và C). Đường thẳng CM cắt đường tròn tâm D tại điểm thứ hai là N. Hai đường thẳng EM và NF cắt nhau tại điểm T. Gọi H là giao điểm của AT và MN.
Chứng minh:
AT = 4AH.
Cho tam giác đều ACB và ACD, cạnh a. Lần lượt lấy B và D làm tâm vẽ hai đường tròn bán kính a. Kẻ các đường kính ABE và ADF. Trên cung nhỏ CE của đường tròn tâm B lấy điểm M (không trùng với E và C). Đường thẳng CM cắt đường tròn tâm D tại điểm thứ hai là N. Hai đường thẳng EM và NF cắt nhau tại điểm T. Gọi H là giao điểm của AT và MN.
Chứng minh:
MNT là tam giác đều.
Cho đường tròn tâm O bán kính R. Lấy ba điểm bất kỳ A, B, C trên đường tròn (O). Điểm E bất kỳ thuôc đoạn thẳng AB (và không trùng với A, B). Đường thẳng d đi qua điểm E và vuông góc với đường thẳng OA cắt đoạn thẳng AC tại điểm F. Chứng minh ∠ BCF + ∠ BEF = 180 °
Cho đường tròn tâm O đường kính AB. Trên bán kính OA, lấy điểm C tùy ý (C khác O và A). Vẽ đường tròn tâm J đường kính AC. Gọi I là trung điểm BC. Qua I vẽ dây cung MN vuông góc BC; AM cắt đường tròn tâm J tại E.
a/ CM CIME nội tiếp.
b/ CM BMCN là hình thoi. Từ đó suy ra ba điểm E, C, N cùng thuộc một đường thẳng.
c/ CM IE là tiếp tuyến của đường tròn tâm J.
d/ Đường tròn tâm M bán kính MI cắt đường tròn tâm O tại P và Q, Gọi H là giao điểm của PQ và MN. Tính tỉ số HM/HN
Cho nửa đường tròn tâm O, đường kính AB và C là điểm thuộc nửa đường tròn (C không trùng với các điểm A và B). Kẻ đường thẳng d là tiếp tuyến tại C của nửa đường tròn (O). trên đường thẳng d và thuộc nửa mặt phẳng có chứa điểm C với bờ là đường thẳng AB, lấy hai điểm D, E sao cho AD song song với BE. Gọi I là trung điểm của đoạn thẳng DE.
a) Chứng minh: OI // AD và AD + BE = 2.OI;
b) Chứng tỏ tam giác AIO và tam giác DIO có diện tích bằng nhau;
c) Vẽ đường tròn tâm I đường kính DE. Chứng tỏ đường tròn (I) đã cho và đường thẳng AB tiếp xúc nhau.
Cho nửa đường tròn tâm O, đường kính AB và C là điểm thuộc nửa đường tròn (C không trùng với các điểm A và B). Kẻ đường thẳng d là tiếp tuyến tại C của nửa đường tròn (O). trên đường thẳng d và thuộc nửa mặt phẳng có chứa điểm C với bờ là đường thẳng AB, lấy hai điểm D, E sao cho AD song song với BE. Gọi I là trung điểm của đoạn thẳng DE.
a) Chứng minh: OI // AD và AD + BE = 2.OI;
b) Chứng tỏ tam giác AIO và tam giác DIO có diện tích bằng nhau;
c) Vẽ đường tròn tâm I đường kính DE. Chứng tỏ đường tròn (I) đã cho và đường thẳng AB tiếp xúc nhau.
Cho hai đường tròn (O) và (O') có cùng bán kính R cắt nhau tại 2 điểm A, B sao cho tâm O nằm trên đường tròn (O') và tâm O' nằm trên đường tròn tâm O. Đường nối tâm OO' cắt AB tại H, cắt đường tròn (O') tại giao điểm thứ 2 là C. Gọi F là điểm đối xứng của B qua O'.
a, CMR AC là tiếp tuyến của (O) và AC vuông góc với BF
b, Trên cạnh AC lấy điểm D sao cho AD = AF. Qua D kẻ đường thẳng vuông góc với OC và cắt OC tại K, cắt AF tại G. Gọi E là giao điểm của AC và BF. CM tứ giác AHO'E, ADKO nội tiếp
c, Tứ giác AHKG là hình gì? Vì sao?
d, Tính diện tích phần chung của hình (O) và (O') the bán kính R
