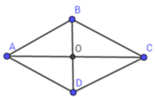
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 10 cm, OA = 6cm. Diện tích hình thoi ABCD là:
A. 48 c m 2
B. 96 c m 2
C. 24 c m 2
D. 40 c m 2
Hai đường chéo AC và BD của hình thoi ABCD cắt nhau tại O. Đường trung trực của AB cắt BD và AC lần lượt ở M và N. Biết BM = 1, AN = 2.Tính diện tích hình thoi ABCD.
cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau taị O. đường thẳng d1 qua O cắt cạnh AB và CD lần lượt tại M và P,đường thẳng d2 qua O cắt cạnh BC và DA lần lượt tại N và Q. BIẾT rằng d1 vuông góc d2.
c/m:
a, tứ giác MNPQ là hình bình hành
b, tứ giác MNPQ là hình thoi.
bài 2:cho tam giác ABC cân tại A. kẻ Bx//AC, Cy// AB, sao cho 2 tia Bx và Cy cắt nhau tại D.
1, C/M tứ giác ABCD là hình thoi
2, các đường trung tuyến BM vàCN của tam giác ABC cắt nhau ở G. AG cắt BC tại O. c/m AO là đường cao của tam giác ABC.
3, C/M A,O,D thẳng hàng.
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O. Biết OA = 12cm, diện tích hình thoi ABCD là 168 c m 2 . Cạnh của hình thoi là:
A. 190 (cm)
B. 180 (cm)
C. 193 (cm)
D. 195 (cm)
Cho hình thoi ABCD có hai đường chéo cắt nhau tại H . Biết AC = 4 cm BD = 3 cm . a/Tính cạnh của hình thoi . b/Kẻ HI vuông góc với AB ,I thuộc AB .Tính HI? c/Kẻ DM vuông góc với AB M thuộc AB .Tính DM ?
Cho hình thoi ABCD có hai đường chéo cắt nhau tại H . Biết AC = 4 cm BD = 3 cm . a/Tính cạnh của hình thoi . b/Kẻ HI vuông góc với AB ,I thuộc AB .Tính HI? c/Kẻ DM vuông góc với AB M thuộc AB .Tính DM ?
Cho hình thoi ABCD có hai đường chéo cắt nhau tại H . Biết AC = 4 cm BD = 3 cm . a/Tính cạnh của hình thoi . b/Kẻ HI vuông góc với AB ,I thuộc AB .Tính HI? c/Kẻ DM vuông góc với AB M thuộc AB .Tính DM ?
Cho hình bình hành ABCD 2 đường chéo cắt nhau tại O. Trên BD lấy hai điểm M và N sao cho BM=DN
a/ C/minh AMCN là hình bình hành
b/ AN kéo dài cắt DC tại I và CM kéo dài cắt AB tại K. Cmr I đối xứng với K qa O
C/ Tìm điều kiện của hbh ABCD để AMCN là hình thoi
d/ Khi BM=DN=1/3 BD. Hãy c/minh K là trung điểm AB và I là trung điểm DC. Tính diện tích BKM nếu diện tích ABCD=60cm2
bài 1:cho tứ giác ABCD có 2 đường chéo ac và bd vuông góc với nhau . gọi m,n,p,q lần lượt là tđ của các cạnh ab,bc,cd,da
a) mnpq là hình j?
b)mnpq là hình vuôn thì abcd cần đk j?
c)cho ac=6cm,bd=8cm. tính diện tích mnpq
bài 2: Cho abc vuông tại a . lấy d thuộc cạnh bc, e là tđ của ac, f đối xứng với d qua e . cm afcd là hbh
bài 3: cho hình thoi abcd . gọi o là giao của 2 đường chéo . qua b vẽ đường thẳng song song với ac, qua c vẽ đường thẳng song song bd . 2 đường thẳng cắt tại k
a) cmr obkc là hcn
b) cmr ab=ok
