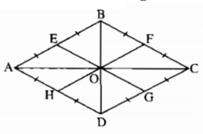
Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).

Đặt OB = OD = a. Hãy chứng minh OE = a. Tương tự, OF = OG = OH = a. Từ đó suy ra sáu điểm E, B, F, G, D, H cùng thuộc một đường tròn (O;a).
Cho hình thoi ABCD có góc A = 60 độ. Gọi O là giao điểm của 2 đường chéo; E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Chứng minh rằng sáu điểm E, B, F, G, D, H thuộc cùng 1 đường tròn
cho hình thoi ABCD có góc A=60.Gọi O là giao điểm của 2 đường chéo.E,F,G,H lần lượt là trung điểm của AB,BC,CD,DA.Cm các điểm E,B,F,G,D,H cùng thuộc một đường tròn
Cho hình thoi ABCD có góc A=60 độ. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
Chứng minh rằng: 6 điểm E, F, G, H, B,D cùng nằm trên 1 đường tròn
Cho hình thoi ABCD , Góc A =60 độ . Gọi E , F ,G,H lần lượt là trung điểm AB BC CD DA . Chứng minh 6 điểm B ,D,E,F,G,H cùng thuộc một đường tròn
Cho hình thoi ABCD có A=60o. Gọi E,F,G,H lần lượt là trung điểm của các cạnh AB, BC, CD, CA. Chứng minh 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn
Bài 1: Cho hình thang cân ABCD (AB//CD;AB⊥CD).Vẽ E đối xứng A qua CD, F đối xứng A qua trung điểm M của CD. Chứng minh A,B,C,D,E,F cùng thuộc một đường tròn.
Bài 2 : Cho hình thoi ABCD , 2 đường chéo cắt nhau tại O. Trên AB,BC lấy các điểm E,F sao cho BE=BF. OE cắt CD tại G, OF cắt AB tại H. Chứng minh E,F,G,H cùng thuộc 1 đường tròn
Mọi người giúp em với ạ, mai e phải nộp rồi :(
cho hình vuông ABCD có chiều dài cạch là a và có O là giao điểm hai đường chéo. Lấy các điểm E;F;G;H trên các cạnh AB,BC,CD,DA tương ứng sao cho AE=BF=CG=DH=x
1) chứng minh 4 điểm E;F;G;H cùng thuộc 1 đường tròn tâm O
2) chứng minh tứ giác EFGH là hình vuông
AI GIẢI GIÚP MIK VỚI
Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BE và CF cắt nhau tại H. Gọi M là giao điểm của EF và BC. Đường thẳng AM cắt đường tròn (O) tại điểm thứ hai là N. Gọi I là trung điểm BC. Đường thẳng MH cắt AI tại G. Chứng minh rằng:
a) Năm điểm E, F, A, H, N cùng thuộc một đường tròn.
b) Bốn điểm G, I, M, N cùng thuộc một đường tròn.
Cho hình thoi ABCD có hai đường chéo cắt nhau tại O. Gọi H, I, K, L lần lượt là hình chiếu của O trên các cạnh AB, BC, CD, DA. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC,CD,DA.
a) Chứng minh rằng bốn điểm H, I, K, L cùng thuộc một đường tròn. Tính bán kính của đường tròn đó trong trường hợp AC=4cm, góc A=60 độ
b) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn. Khi đó, tìm điều kiện của hình thoi để hai đỉnh B, D cũng thuộc đường tròn đó.