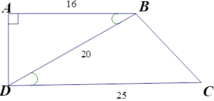
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 90 ∘ nên DBC = 90 ∘ . Theo định lí Pytago, ta có
B C 2 = C D 2 - B D 2 = 25 2 - 20 2 = 152 . Vậy BC = 15cm
Đáp án: C

Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 90 ∘ nên DBC = 90 ∘ . Theo định lí Pytago, ta có
B C 2 = C D 2 - B D 2 = 25 2 - 20 2 = 152 . Vậy BC = 15cm
Đáp án: C
Cho hình thang vuông ABCD (A = D = 90 ∘ ) có BC ⊥ BD, AB = 4cm, CD = 9cm. Độ dài BD là:
A. 8cm
B. 12cm
C. 9cm
D. 6cm
Bài 1: Hình thang ABCD (AB//CD) có AB=AD+BC. Chứng minh rằng các tia phân giác của các góc C và D gặp nhau tại 1 điểm thuộc đáy AB
Bài 2: Hình thang vuông ABCD (góc A = góc D= 90°)có AB =4cm, CD=9cm, BC=13cm. Tính AD
Bài 3: hình thang vuông ABCD (góc A=góc D=90°)có AB =9cm,CD=15cm, AC=17cm. Tính độ dài cạnh bên
Cho hình thang vuông ABCD (A = D = 90 ∘ ) có AB = 16cm, CD = 25cm, BD = 20cm. Tam giác ABD đồng dạng với tam giác nào dưới đây?
A. ΔBDC
B. ΔCBD
C. ΔBCD
D. ΔDCB
cho hình thang ABCD(AB<CD) (AB//CD) biết BD vuông góc với BC,BH là đường cao.BC=15cm,BH=12cm,BD=20cm,DC=25cm.
tính diện tích hình thang ABCD
Cho hình thang ABCD có góc A=góc D=90 độ, đáy AB và CD. Tính BC khi AB=12cm, AD= 15cm,AC=25cm
Cho hình thang vuông ABCD. Góc A=góc D (=90 độ). Biết AB=9cm; CD=16cm; BC=25cm. Trên BC lấy E sao cho BE=BA. Tính:
a) Góc AED
b) Diện tích ABCD; diện tích tam giác AED
Hình thang vuông ABCD (góc A =gióc D=90°) có AB=9cm, CD=15cm, AC=17cm. Tính độ dài các cạnh bên
hình thang vuông ABCD (góc A=góc D=90°)có AB =9cm,CD=15cm, AC=17cm. Tính độ dài cạnh bên
cho hình thang vuông ABCD [góc A=D=90 độ].AB=9cm,CD=15cm,AC=17cm.Tính độ dài các cạnh bên