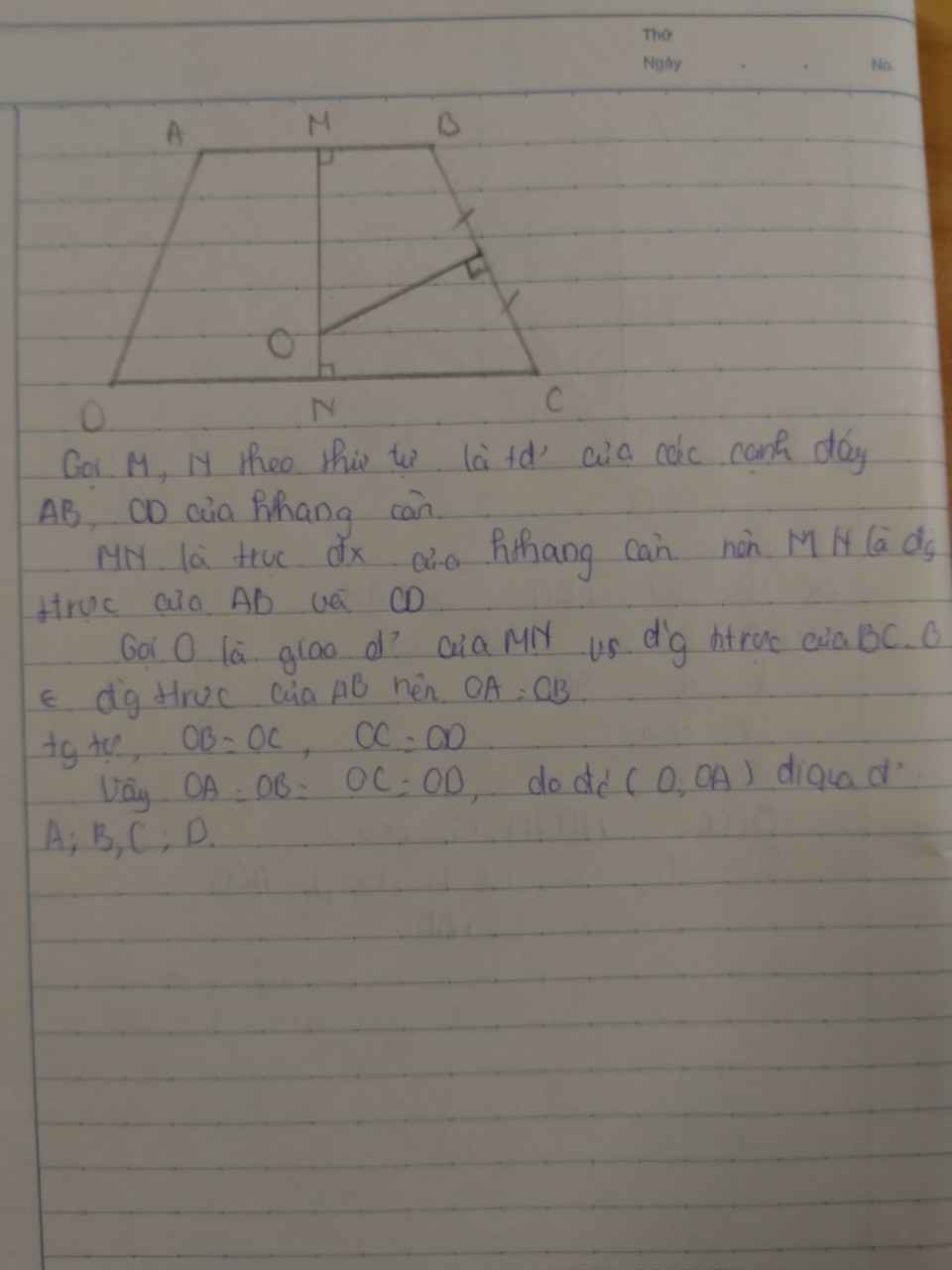Question

Cho hình thang cân ABCD. Chứng minh rằng tồn tại một đường tròn đi qua cả bốn đỉnh của hình thang.

Answer 1

OA=oB=oc=od,(O,OA)di qua cac diem a,b,c,d

Answer 2

Answer 3

Gọi $O=d\cap d^{\prime }$ ta có:

$d$ là trục của hình thang cân $ABCD\Rightarrow d$ là đường trung trực của AB và CD.

Mà $O\in d\Rightarrow \{\begin{array}{c}OA=OB\\ OC=OD\end{array}\left(1\right)$ (điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó).

Lại có $O\in d^{\prime }\Rightarrow OA=OD\left(2\right)$ (điểm thuộc trung trực của một đoạn thẳng cách đều 2 đầu mút của đoạn thẳng đó).

Từ (1) và (2) $\Rightarrow OA=OB=OC=OD$.

Vậy bốn điểm $A,B,C,D$ cùng thuộc đường tròn tâm $O$, bán kính $R=OA=OB=OC=OD$.

Answer 4

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 5

gọi M,N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và CD

gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA=OB

Tương tự OB =OC,OC=OD

Vậy OA=OB=OC=OD, dó đó (O;OA)đi qua các điểm A,B,C,D

Answer 6

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

=>MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

                   

Answer 7

   
 

Answer 8

Gọi M, N là trung điểm của AB và CD là đáy của hình thang cân 

MN là trục đối xứng của hình thang cân ⇒ MN cũng là đường trung trực của AB và CD 

⇒MN vuông góc với AB và CD 

Gọi O là giao điểm của MN với đường trung trực của BC 

Có O ϵ MN mà MN là đường trung trực của AB ⇒ OA=OB (1)

Có Oϵ MN mà MN cũng là đường trung trực của BC ⇒ OB =OC (2)

Có Oϵ MN mà MN cũng là đường trung trực của Dc ⇒ OD=OC(3) 

Từ 1,2,3, ⇒ OA=OB=OC=OD⇒ A,B,C,D cùng thuộc ( O;OA) 

Answer 9

  

Answer 10

gọi tâm đường tròn đó là O

=>(O;OA) đi qua bốn điểm A,B,C,D

Answer 11

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 12

 

Answer 13

Answer 14

OA=OB=OC=OD,(O;OA) đi qua các điểm a,b,c,d

Answer 15

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

   

Answer 16

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 17

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 18

A,B,C,D cùng thuộc một đường tròn

Answer 19

Hạ OH $\perp$ BN, OK $\perp$ AM. Chứng minh $\Delta COK=\Delta COH$ suy ra OC là đường phân giác của tam giác AOB.

  Bạn vẫn chưa trả lời bài tập này. Gửi câu trả lời!

Answer 20

Gọi M ,N lần lượt là trung điểm của các cạnh đáy AB,CD của hìn thang cân. MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và CD.

GỌi O là giao điểm của MN với đường trung trực của BC

O thuộc đường trung trực của AB nên OA = OB

O thuộc đường trung trực của BC nên OB = OC

O thuộc đường trung trực của CD nên OC =OD

⇒OA=OB=OC=OD

Do đó (O;OA) đi qua các điểm A,B,C,D.

Answer 21

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 22

Gọi M,N lần lượt là trung điểm của AB và CD MN là trục đối xứng của hình thang cân ABCD nên MN là đường trung trực của AB và CD Gọi O là giao điểm của MN với tryng trực BC. O thuộc trung trực AB nên OA= OB . Tương tự ta cũng có OB=OC, OC=OD Vậy OA=OB=OC=OD do đó( O;OA) đi qua các điểm A,B,C,D

Answer 23

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 24

Gọi M là trung điểm của AB , N là trung điểm của CD 

=> MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và CD 

Gọi O là giao điểm MN vs đường trung trực BC , O thuộc đường trung trực AB nên OA = OB 

Cmtt  OB = OC  , OC = OB 

=> OA = OB =OC =OD , do đó ( O ; OA ) đi qua bốn điểm A , B , C , D 

 

 

Answer 25

OA=OB=OC=OD(O;OA) đi qua các điểm A,B,C,D

Answer 26

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

Answer 27

Gọi M, N theo thứ tự là trung điểm của các cạnh đáy AB, CD của hình thang cân.

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và của CD.

Gọi O là giao điểm của MN với đường trung trực của BC. O thuộc đường trung trực của AB nên OA = OB.

Tương tự, OB = OC, OC = OD.

Vậy OA = OB = OC = OD, do đó (O ; OA) đi qua các điểm A, B, C, D.

                   

Answer 28

OA=OB=OC=OD⇒A,B,C,D ϵ (O;OA)

Answer 29

 

Answer 30

Gọi M theo thứ tư trung điểm của cá cạnh đáy AB,CD của hình thang cân

MN là trục đối xứng của hình thang cân nên MN là đường trung trực của AB và CD

Gọi O là giao diểm của MN với đường trung trục BC 

O thuộc đường trung trực AB nên OA=OB

 tương tự OB=OC,OC=OD

Vậy OA=OB=ÔC=OD do đó( O;OA) đi qua bốn điếm A,B,C,D