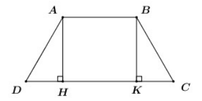
Kẻ AH, BK cùng cuông góc với CD (H, K CD)
Xét tứ giác ABKH có: A B / / H K A H / / B K , suy ra ABKH là hình bình hành.
Lại có A H K ^ = 90 0 nên ABKH là hình chữ nhật, do đó HK = AB = 4
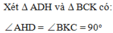
AD = BC (tính chất hình thang cân)
A D H ^ = A C K ^ = ACK (tính chất hình thang cân)
⇒ ∆ A D H = ∆ B C K (cạnh huyền – góc nhọn)
=> DH = CK (hai cạnh tương ứng)
Mà DH + CK = CD – HK = 8 – 4 = 4
Do đó DH = CK = 2
Áp dụng định lý Py-ta-go trong tam giác vuông ADH ta có:
![]()
Vậy diện tích hình thang ABCD là:

Đáp án cần chọn là: B












