Question

Cho hình thang ABCD ( AB//CD). Gọi M;N;P;Q theo thứ tự là trung điểm của các cạnh AB;AC;CD;BD.
a/ Tứ giác MNPQ là hình gì?
b/ Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi?
c/ Khi ABCD là hình thang cân có hai đường chéo vuông góc thì MNPQ là hình gì?

Answer 1

a / hình bình hành 

b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD

c/hình vuông

Answer 2

(Hình thì bạn tự vẽ nha)
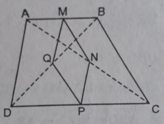
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD  (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD                                 (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC                                                        (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN 
=> MNPQ là hình thoi

 

Answer 3

Do AI, DI lần lượt là phân giác BADˆ;ADCˆ→IADˆ=BADˆ2 và IDAˆ=ADCˆ2

Ta có AIDˆ=180o−(IADˆ+IDAˆ)=180o−BADˆ+ADCˆ2=180o−180o2=90o

Xét Δ AID vuông tại I có IM là trung tuyến thuộc cạnh huyền AD  MA=MI 

=> Δ AMI cân tại M => MAIˆ=MIAˆ

Do MAIˆ=BAIˆ→BAIˆ=MIAˆ

Mà 2 góc ở vị trí so le trong  MI // AB (1)

Tương tự có NJ // AB (2) 

Lại có MN // AB (3) ( MN là đường trung bình của hình thang ABCD ) 

Từ (1); (2) và (3)=>  M, N, I, J thẳng hàng.

Answer 4

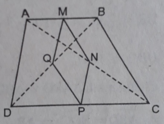
a) Xét tam giác BAD có: MB=MA ; QB=QD

=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD  (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD                                 (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC                                                        (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN 
=> MNPQ là hình thoi