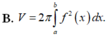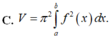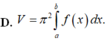Question

cho hình phẳng giới hạn bởi đồ thị hàm số \(y=4xe^{2x}\), trục hoành và các đương thẳng x=3,x=5. Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox

Answer 1

Thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox là \(V=\pi\int_3^5\left(4xe^{2x}\right)^2dx=16\pi\int_3^5x^2e^{4x}dx\)

Gọi \(I=\int x^2e^{4x}dx\)

Đặt \(\left\{{}\begin{matrix}u=x^2\\dv=e^{4x}dx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=\dfrac{1}{4}e^{4x}\end{matrix}\right.\)

\(\Rightarrow I=x^2.\dfrac{1}{4}e^{4x}-\int\dfrac{1}{4}e^{4x}.2xdx=x^2.\dfrac{1}{4}e^{4x}-\dfrac{1}{2}\int xe^{4x}dx\)

Gọi \(K=\int xe^{4x}dx\)

Đặt \(\left\{{}\begin{matrix}u=x\\dv=e^{4x}dx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=dx\\v=\dfrac{1}{4}e^{4x}\end{matrix}\right.\)

\(\Rightarrow K=x.\dfrac{1}{4}e^{4x}-\int\dfrac{1}{4}e^{4x}dx=x.\dfrac{1}{4}e^{4x}-\dfrac{1}{16}e^{4x}\)

\(\Rightarrow I=\dfrac{x^2e^{4x}}{4}-\dfrac{xe^{4x}}{8}+\dfrac{e^{4x}}{32}+C\)

\(\Rightarrow V=16\pi\left(\dfrac{25e^{20}}{4}-\dfrac{5e^{20}}{8}+\dfrac{e^{20}}{32}-\dfrac{9e^{12}}{4}+\dfrac{3e^{12}}{8}-\dfrac{e^{12}}{32}\right)\)

\(=16\pi\left(\dfrac{181e^{20}}{32}-\dfrac{61e^{12}}{32}\right)=\pi\dfrac{181e^{20}-61e^{12}}{2}\)