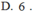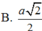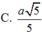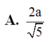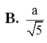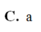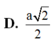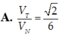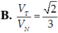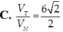Chọn A.
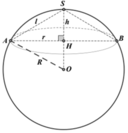
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
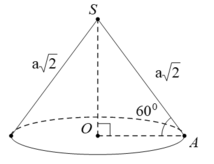
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1.
Suy ra: ![]()
Góc ở đỉnh của hình nón là ∠ A S B = 2 ∠ A S H = 120 ° nên suy ra H ∈ S O (như hình vẽ).
Trong tam giác OAH vuông tại H ta có:
![]()
![]()
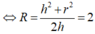
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.
Cách 2:
Gọi O, R lần lượt là tâm và bán kính của mặt cầu.
Đường tròn đáy của hình nón có tâm H bán kính r.
Do H là hình chiếu của S và O trên mặt đáy của hình nón nên S, H, O thẳng hàng.
Hình nón có độ dài đường sinh l=2, đường cao h=1.
Trong tam giác SAH vuông tại H ta có:
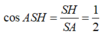
![]()
Xét tam giác SOA có OS=OA=R và OSA= 60 °
Suy ra tam giác SOA đều.
Do đó R=OA=SA=2.
Vậy đường kính mặt cầu chứa điểm S và đường tròn đáy hình nón bằng 4.