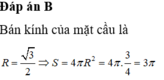Các câu hỏi tương tự
Cho hình lập phương ABCD.ABCD có cạnh bằng
2
a
2
Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.ABCD Khi đó
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2 a 2 Gọi S là tổng diện tích tất cả các mặt của bát diện có các đỉnh là tâm của các mặt của hình lập phương ABCD.A'B'C'D' Khi đó
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8
π
Tính chiều cao của hình nón này.
Đọc tiếp
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Xét tứ diện AB’CD’. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Xét tứ diện AB’CD’. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được.
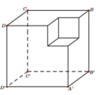
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt Tính bán kính của (S).
Đọc tiếp
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt 
Tính bán kính của (S).
Một thùng hình trụ có thể tích bằng 12 π , chiều cao bằng 3. Diện tích xung quang của thùng đó là:
A. 12 π
B. 6 π
C. 16 π
D. 18 π
Một vật thể nằm giữa hai mặt phẳng x -1 và x 1 thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x (-1
≤
x
≤
1) là một hình tròn có diện tích bằng 3
π
Thể tích của vật thể bằng A. 3
π
2
B. 6
π
C. 6 D. 2
π
Đọc tiếp
Một vật thể nằm giữa hai mặt phẳng x = -1 và x = 1 thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x (-1 ≤ x ≤ 1) là một hình tròn có diện tích bằng 3 π Thể tích của vật thể bằng
A. 3 π 2
B. 6 π
C. 6
D. 2 π
Tổng các nghiệm của phương trình 2cos3x(2cos2x+1) 1 trên đoạn [-4
π
;6
π
] A.61
π
B. 72
π
C. 50
π
D. 56
π
Đọc tiếp
Tổng các nghiệm của phương trình 2cos3x(2cos2x+1)= 1 trên đoạn [-4 π ;6 π ]
A.61 π
B. 72 π
C. 50 π
D. 56 π
Cho phương trình cos5x.cosx cos4x.cos2x + 3cos2x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là: A. B. C. D.
Đọc tiếp
Cho phương trình cos5x.cosx = cos4x.cos2x + 3cos2x + 1. Các nghiệm thuộc khoảng (-π; π) của phương trình là:
A. 
B. 
C. 
D. 