Góc giữa AB và DD' = góc giữa AB và AA' ( vì DD'=AA')
Nên bằng 90 độ
\(\widehat{\left(AB,DD'\right)}=\widehat{\left(AB,AA'\right)}=\widehat{BAA'}=90^o\) do DD'//AA'.
Góc giữa AB và DD' = góc giữa AB và AA' ( vì DD'=AA')
Nên bằng 90 độ
\(\widehat{\left(AB,DD'\right)}=\widehat{\left(AB,AA'\right)}=\widehat{BAA'}=90^o\) do DD'//AA'.
cho hình lập phương abcd.a'b'c'd' gọi I là trung điểm cạnh AB. Tính cosin của góc giữa hai đường thẳng A'D và B'I được kết quả là
Cho hình lập phương ABCD.A'B'C'D'. GÓC GIỮA HAI ĐƯỜNG THẲNG AD và A'C' là
Cho hình chóp S.ABC có AB = AC, S A C ^ = S A B ^ . Tính số đo của góc giữa hai đường thẳng SA và BC
A . 45 0
B . 60 0
C . 30 0
D . 90 0
Cho hình lập phương ABCD.A’B’C’D’. Hãy nêu tên các đường thẳng đi qua hai đỉnh của hình lập phương đã cho và vuông góc với:
a) đường thẳng AB
b) đường thẳng AC
Cho hình chóp S. ABC có AB=AC, S A C ^ = S A B ^ . Tính số đo của góc giữa hai đường thẳng SA và BC
A. 45 °
B. 60 °
C. 30 °
D. 90 °
Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP
A. 60 0
B. 90 0
C. 30 0
D. 45 0
Cho hình lập phương ABCD.A'B'C'D'. Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C). Tính số đo góc giữa hai mặt phẳng (BA'C) và (DA'C).
A. 60°
B. 135°
C. 150°
D. 90°
Cho hình lập phương ABCD. A’B’C’D’ cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A’D.
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 4
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Góc giữa hai đường thẳng AB′ và BC′ bằng (tham khảo hình vẽ bên).
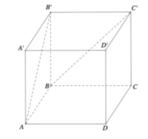
A. 6 0 o
B.9 0 o
C. 45 o
D. 3 0 o