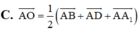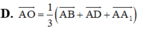Các câu hỏi tương tự
Cho hình lập phương
A
B
C
D
.
A
1
B
1
C
1
D
1
. Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng: A.
A
O
→
1
3
A
B
→
+...
Đọc tiếp
Cho hình lập phương A B C D . A 1 B 1 C 1 D 1 . Gọi O là tâm của hình lập phương. Chọn đẳng thức đúng:
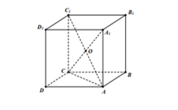
A. A O → = 1 3 A B → + A D → + A A 1 →
B. A O → = 1 2 A B → + A D → + A A 1 →
C. A O → = 1 4 A B → + A D → + A A 1 →
D. A O → = 2 3 A B → + A D → + A A 1 →
Cho hình lập phương ABCD.A′B′C′D′. Gọi O là tâm của hình vuông ABCD. Côsin của góc giữa hai mặt phẳng (OA′B′) và (OC′D′) bằng
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′. Gọi O là tâm của hình vuông ABCD. Côsin của góc giữa hai mặt phẳng (OA′B′) và (OC′D′) bằng
![]()
![]()
![]()
![]()
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.a) Hãy biểu diễn các vectơ
A
O
→
,
A
O
→
, theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.b) Chứng minh rằng
A
D
→...
Đọc tiếp
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ A O → , A O ' → , theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng A D → + D ' C ' → + D ' A ' → = A B →
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S sao cho Tính độ dài đoạn OS theo a.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S sao cho ![]() Tính độ dài đoạn OS theo a.
Tính độ dài đoạn OS theo a.
![]()
![]()
![]()
![]()
Cho hình lập phương AbCD.ABCD có cạnh bằng a. Gọi O là tâm hình vuông ABCD, S là điểm đối xứng với O qua CD (tham khảo hình vẽ bên). Thể tích của khối đa diện ABCDSABCD bằng A.
2
a
3
3
B.
3
a
3...
Đọc tiếp
Cho hình lập phương AbCD.A'B'C'D' có cạnh bằng a. Gọi O là tâm hình vuông ABCD, S là điểm đối xứng với O qua CD' (tham khảo hình vẽ bên). Thể tích của khối đa diện ABCDSA'B'C'D' bằng

A. 2 a 3 3
B. 3 a 3 2
C. 7 a 3 6
D. 4 a 3 3
Cho hình lập phương ABCD.ABCD có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuôngABCD. Kết quả tính diện tích toàn phần
S
t
p
của khối nón đó có dạng
πa
2
4
(
b
+
c...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh a. Một khối nón có đỉnh là tâm của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuôngA'B'C'D'. Kết quả tính diện tích toàn phần S t p của khối nón đó có dạng πa 2 4 ( b + c ) với b và c là hai số nguyên dương và b>1. Tính bc
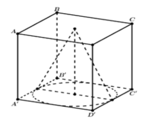
A. bc=5
B. bc=7
C.bc=8
D.bc=15
Cho hình lập phương ABCD.ABCD có cạnh bằng a . Gọi O và O lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B C và CD. Tính thể tích khối tứ diện OOMN
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
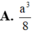
![]()
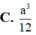
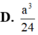
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn
O
S
→
O
A
→
+
O
B
→
+
O
C
→
+
O
D
→...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi O là tâm hình vuông ABCD và điểm S thỏa mãn O S → = O A → + O B → + O C → + O D → + O A ' → + O B ' → + O C ' → + O D ' → . Tính độ dài đoạn OS theo a
A. OS=6a.
B. OS=4a.
C. OS=a.
D. OS=2a.
Cho hình lập phương ABCD. A ‘B’C’D’ có độ dài cạnh bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, C’D’ và DD’. Tính thể tích khối tứ diện MNPQ A.
3
8
B.
1
8
C.
1
12
D.
1
24
Đọc tiếp
Cho hình lập phương ABCD. A ‘B’C’D’ có độ dài cạnh bằng 1. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, C’D’ và DD’. Tính thể tích khối tứ diện MNPQ
A. 3 8
B. 1 8
C. 1 12
D. 1 24