Phương pháp:
Sử dụng công thức tính thể tích khối chóp V = 1 3 S đ á y . h
Cách giải:
Ta có:

Chọn: A
Phương pháp:

Sử dụng công thức tính thể tích khối chóp V = 1 3 S đ á y . h
Cách giải:
Ta có:

Chọn: A
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 72 cm3. Gọi M là trung điểm của đoạn thẳng BB’. Tính thể tích khối tứ diện ABCM.
![]()
![]()
![]()
![]()
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, BAC = 30 ° , AB = a 3 , AA' = a. Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'.
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho khối lăng trụ ABC.A′B′C′ có thể tích bằng 1. Gọi M,N lần lượt là trung điểm của các đoạn thẳng AA′ và BB′. Đường thẳng CM cắt đường thẳng C′A′ tại P, đường thẳng CN cắt đường thẳng C′B′ tại Q. Thể tích của khối đa diện lồi A′MPB′NQ bằng
Cho mình hỏi sao suy ra được A′C′=A′P,C′B′=B′Q vậy ạ

Cho hình lăng trụ ABC.A'B'C', M là trung điểm của CC'. Mặt phẳng (ABM) chia khối lăng trụ thành hai khối đa diện. Gọi V 1 là thể tích khối đa diện chứa đỉnh C và V 2 là thể tích khối đa diện còn lại. Tính tỉ số V 1 V 2 .
![]()
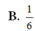
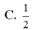
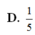
Cho khối lăng trụ ABC.A'B'C', hình chiếu của điểm A lên mặt phẳng (A'B'C') là trung điểm M của cạnh B'C' và A'M=a 3 , hình chiếu của điểm A lên mặt phẳng (BCC'B') là H sao cho MH song song với BB' và AH=a, khoảng cách giữa hai đường thẳng BB' , CC' bằng 2a . Thể tích khối lăng trụ đã cho là
A. 3 2 a 3
B. 2 a 3
C. 2 2 a 3 3
D. 3 2 a 3 2
Cho hình lăng trụ ABC.A’B’C’ có thể tích bằng V. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, A’C’, BB’. Thể tích của khối tứ diện CMNP bằng:
A. 5 24 V
B. 1 4 V
C. 7 24 V
D. 1 3 V
Cho khối lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông cân tại C, AB = 2a. Trên các đoạn thẳng AB′, A′C có lần lượt các điểm M, N và P, Q sao cho MNPQ là tứ diện đều. Tính thể tích của khối lăng trụ ABC.A′B′C′.
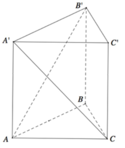
![]()
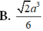
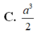
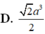
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M là trung điểm cạnh B B ' , điểm N thuộc cạnh CC' sao cho C N = 2 C ' N . Tính thể tích khối chóp A.BCNM theo V


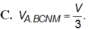

Cho hình lăng trụ tam giác đều ABC.A'B'C' có AA' = a 3 , AB = a. Gọi M là trung điểm BC. Tính thể tích V của hình chóp AMB’C’.
A. V = a 3 3 4
B. V = a 3 3
C. V = a 3 4
D. V = a 3 3 2