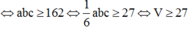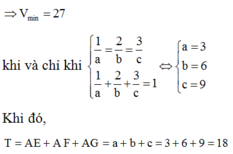Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).
Trong không gian Oxyz, cho mặt phẳng (P) thay đổi nhưng luôn đi qua hai điểm là A(2;0;0), M(1;1;1). Cho (P) cắt các tia Oy, Oz lần lượt tại các điểm B, C (khác O). Viết phương trình mặt phẳng (P) sao cho thể tích của từ diện OABC nhỏ nhất. A.
x
2
+
y
3
+
z
6
1
B.
x
2...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P) thay đổi nhưng luôn đi qua hai điểm là A(2;0;0), M(1;1;1). Cho (P) cắt các tia Oy, Oz lần lượt tại các điểm B, C (khác O). Viết phương trình mặt phẳng (P) sao cho thể tích của từ diện OABC nhỏ nhất.
A. x 2 + y 3 + z 6 = 1
B. x 2 + y 4 + z 4 = 1
C. x 2 + y 6 + z 3 = 1
D. 2x-y-z-2=0
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;1). Mặt phẳng (P) thay đổi đi qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C khác gốc tọa độ. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC
A. 18
B. 9
C. 6
D. 54
Cho điểm M(1;2;1). Mặt phẳng (P) thay đổi đi qua M lần lượt cắt tia Ox, Oy, Oz tại A, B, C. Giá trị nhỏ nhất của thể tích khối tứ diện OABC là
Đọc tiếp
Cho điểm M(1;2;1). Mặt phẳng (P) thay đổi đi qua M lần lượt cắt tia Ox, Oy, Oz tại A, B, C. Giá trị nhỏ nhất của thể tích khối tứ diện OABC là
![]()
![]()
![]()
![]()
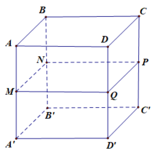
Cho hình hộp ABCD.ABCD có AB AD 2a, AA 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.ABCD nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích
V
T
V
C
giữa khối cầu và khối trụ là.
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có AB = AD = 2a, AA' = 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.A'B'C'D' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V T V C giữa khối cầu và khối trụ là.
![]()
![]()
![]()
Cho hình hộp chữ nhật ABCD.ABCD có
A
B
B
C
a
;
A
A
a
3
. Gọi I là giao điểm của AD và A’D ; H là hình chiếu của I trên mặt phẳng
A
B
C
D
, K là hình chiếu của B lên mặt phẳng...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A B = B C = a ; A ' A = a 3 . Gọi I là giao điểm của AD' và A’D ; H là hình chiếu của I trên mặt phẳng A ' B ' C ' D ' , K là hình chiếu của B lên mặt phẳng C A ' B ' . Tính thể tích khối tứ diện IHBK ?
A. a 3 3 4
B. a 3 3 6
C. a 3 3 16
D. a 3 3 8
Cho hình hộp
A
B
C
D
.
A
B
C
D
có
A
B...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a Lấy M, N, P, Q lần lượt là trung điểm của A A ' , B B ' , C C ' , D D ' Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ A B C D . M N P Q nội tiếp mặt cầu (C) Tỉ số thể tích V ( T ) V ( C ) giữa khối trụ và khối cầu là:
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho hình hộp
A
B
C
D
.
A
B
C
D
có
A
B
A
D
2
a
,...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có A B = A D = 2 a , A A ' = 4 a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’,CC, DD’. Biết hình hộp chữ nhật A B C D . A ' B ' C ' D ' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích V ( T ) V ( C ) giữa khối cầu và khối trụ là
A. 2 3 3
B. 3 3
C. 2 3 3
D. 1 3 2
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA SB 3 cm, BC 5cm và diện tích tam giác SAC bằng 6
c
m
2
. Một mặt phẳng
α
thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS, AB, AC lần lượt tại M, N, P. Tính giá trị nhỏ nhất
T
m
của biểu thức
T
1...
Đọc tiếp
Cho tứ diện SABC có SA vuông góc với mặt phẳng (ABC), SA= SB= 3 cm, BC =5cm và diện tích tam giác SAC bằng 6 c m 2 . Một mặt phẳng α thay đổi qua trọng tâm G của tứ diện cắt các cạnh AS, AB, AC lần lượt tại M, N, P. Tính giá trị nhỏ nhất T m của biểu thức T = 1 A M 2 + 1 A N 2 + 1 A P 2
A. T m = 8 17
B. T m = 41 144
C. T m = 1 10
D. T m = 1 34