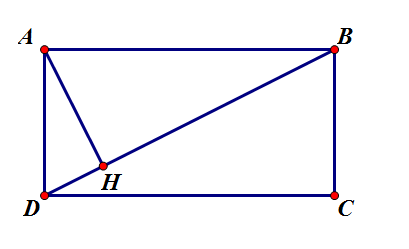
Cho hình chữ nhật ABCD. Vẽ đường cao AH của tam giác ABD
a) cm tam giác HBA đồng dạng tam giác CDB
b) Cm AD2 = DH.DB; AH2= HD. HB
bài giải
a)Xét Δ HBA và ΔABD có:
góc AHB=góc DAB=90 độ
góc B chung
=> Δ HBA đồng dạng Δ ABD (g-g)
b) xét ΔHDA và Δ ADB có
góc AHD = góc DAB =90 độ
góc D chung
=> Δ HDA đồng dạng Δ ADB(g-g)
=>\(\dfrac{HD}{AD}=\dfrac{DA}{DB}=\dfrac{HA}{AB}\)=>\(\dfrac{HD}{AD}=\dfrac{DA}{DB}\)=>AD2=HD.BD
a) Xét \(\Delta HBA\) và \(\Delta CDB\) có:
\(\widehat{HBA}=\widehat{CDB}\) (so le trong)
\(\widehat{AHB}=\widehat{BCD}=90^0\)
\(\Rightarrow\Delta HBA\sim\Delta CDB\left(g-g\right)\)
b) Xét \(\Delta ADB\) và \(\Delta HDA\) có:
\(\widehat{D}\) chung
\(\widehat{DAB}=\widehat{DHA}=90^0\)
\(\Rightarrow\Delta ADB\sim\Delta HDA\left(g-g\right)\) (1)
\(\Rightarrow\dfrac{AD}{DH}=\dfrac{DB}{AD}\Rightarrow AD.AD=DH.DB\)
Hay \(AD^2=DH.DB\)
Xét \(\Delta ADB\) và \(\Delta HAB\) có:
\(\widehat{B}\) chung
\(\widehat{BAD}=\widehat{AHB}=90^0\)
\(\Rightarrow\Delta ADB\sim\Delta HAB\left(g-g\right)\) (2)
Từ (1) và (2) suy ra \(\Delta HDA\sim\Delta HAB\)
\(\Rightarrow\dfrac{HD}{AH}=\dfrac{AH}{HB}\Rightarrow HD.HB=AH.AH\)
Hay \(AH^2=HD.HB\)